| Beobachtung | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 1 | 2 | 6 | 2 | 5 | 2 | 4 | 3 | 1 | 3 | 2 | 1 | 2 | 3 | 4 | 1 | 2 |
| Y | 1 | 2 | 6 | 2 | 5 | 2 | 4 | 3 | 1 | 3 | 2 | 1 | 21 | 3 | 4 | 1 | 2 |
4 Lagemaße
Ein Lagemaß ist eine Zahl, die etwas darüber aussagt, wo das Zentrum einer Verteilung auf der Zahlengeraden liegt. Es gibt verschiedene Lagemaße. Welches von diesen Maßen in einem konkreten Fall sinnvoll anzuwenden ist, hängt vom Kontext und dem Skalenniveau ab.
4.1 Arithmetisches Mittel
Das geläufigste Lagemaß ist das arithmetische Mittel oder kurz der Mittelwert. Es ist nichts anderes als die Summe aller beobachteten Werte geteilt durch die Anzahl der Beobachtungen. Dementsprechend kann man das arithmetische Mittel nur für metrische Merkmale berechnen (also für Merkmale, die mindestens intervallskaliert sind).
Definition (Arithmetisches Mittel):
Für die \(n\) Zahlen \(x_1, x_2, \dots, x_n\) wird der Wert \[ \bar{x} = \frac{1}{n}\left(x_1 + x_2 + \dots + x_n\right) = \frac{1}{n} \sum_{j=1}^n x_j \] arithmetisches Mittel oder kurz Mittelwert genannt.
Das arithmetische Mittel \(\bar{x}\) besitzt zwei wichtige Eigenschaften:
Das arithmetische Mittel minimiert die Summe der quadrierten Abstände: \[ \bar{x} = \underset{a}{\operatorname{argmin}} \sum_{j-1}^n (x_j - a)^2. \] .
Wenn man sich vorstellt, dass jedem Wert \(x_j\) eine Kugel entspricht, die an der Stelle \(x_j\) an eine gewichtslose Stange gehängt wird, dann ist \(\bar{x}\) die Stelle, an der man die Stange auf einem Finger balancieren kann (also der Schwerpunkt).
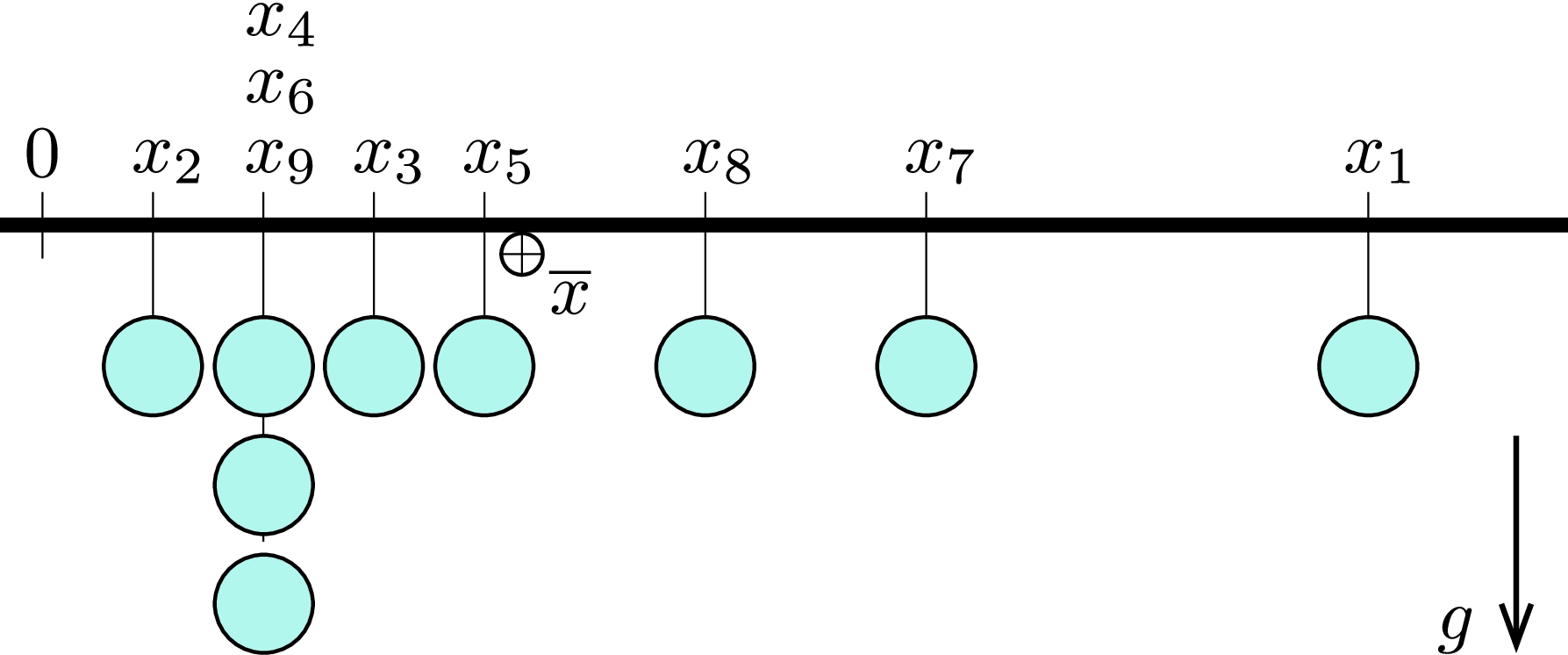
Beispiel Arithmetisches Mittel:
Wir betrachten einen Datensatz mit \(n = 17\) Beobachtungen der zwei Merkmale \(X\) und \(Y\) mit den Werten
Für die arithmetischen Mittel der beiden Merkmale ergibt sich folgende Situation:
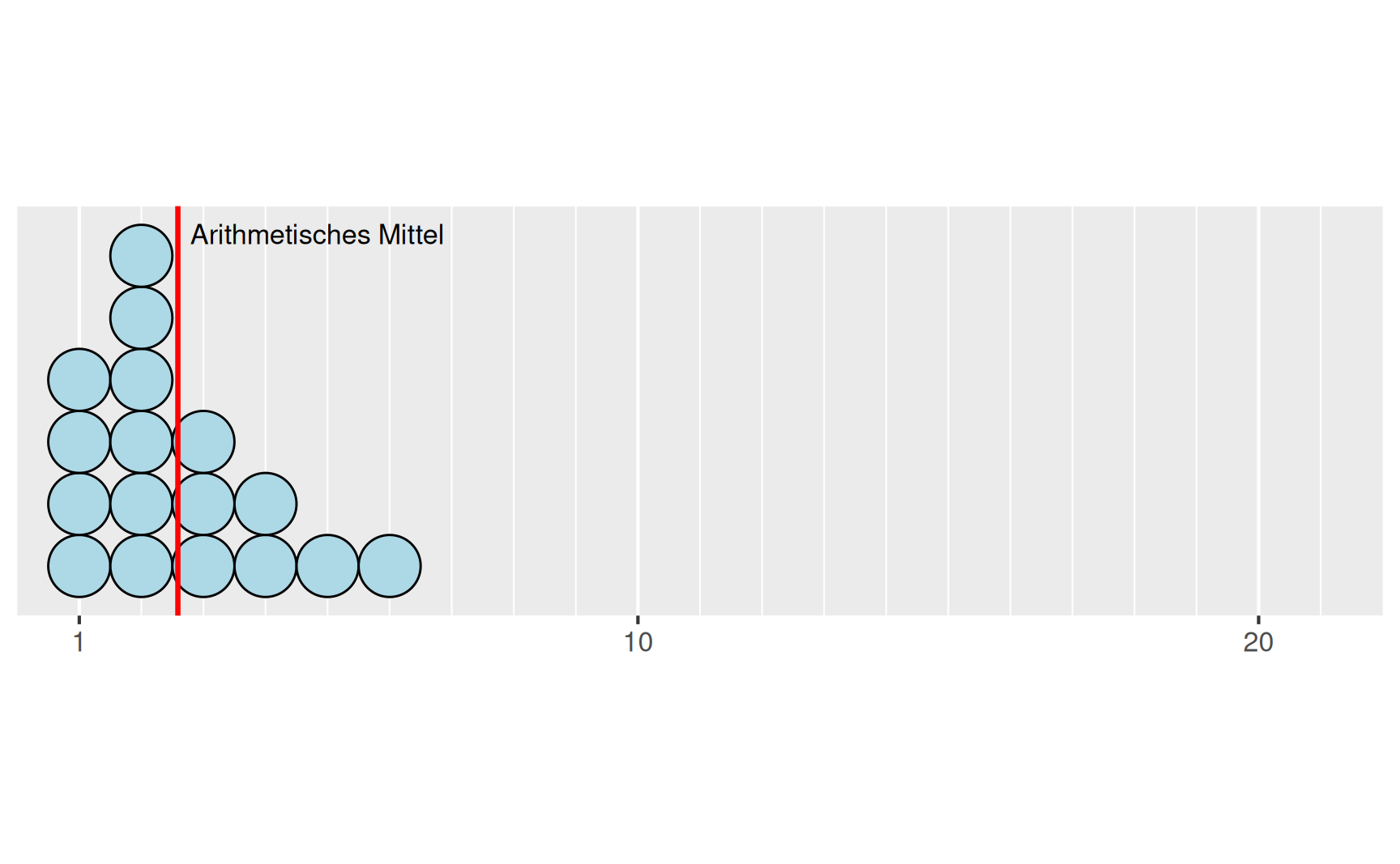
Arithmetisches Mittel von Merkmal \(X\) \[ \bar{x} = \frac{1}{17}(1 + 2 + 6 + \dots + 2 + \dots + 2) = 2.588\dots \]
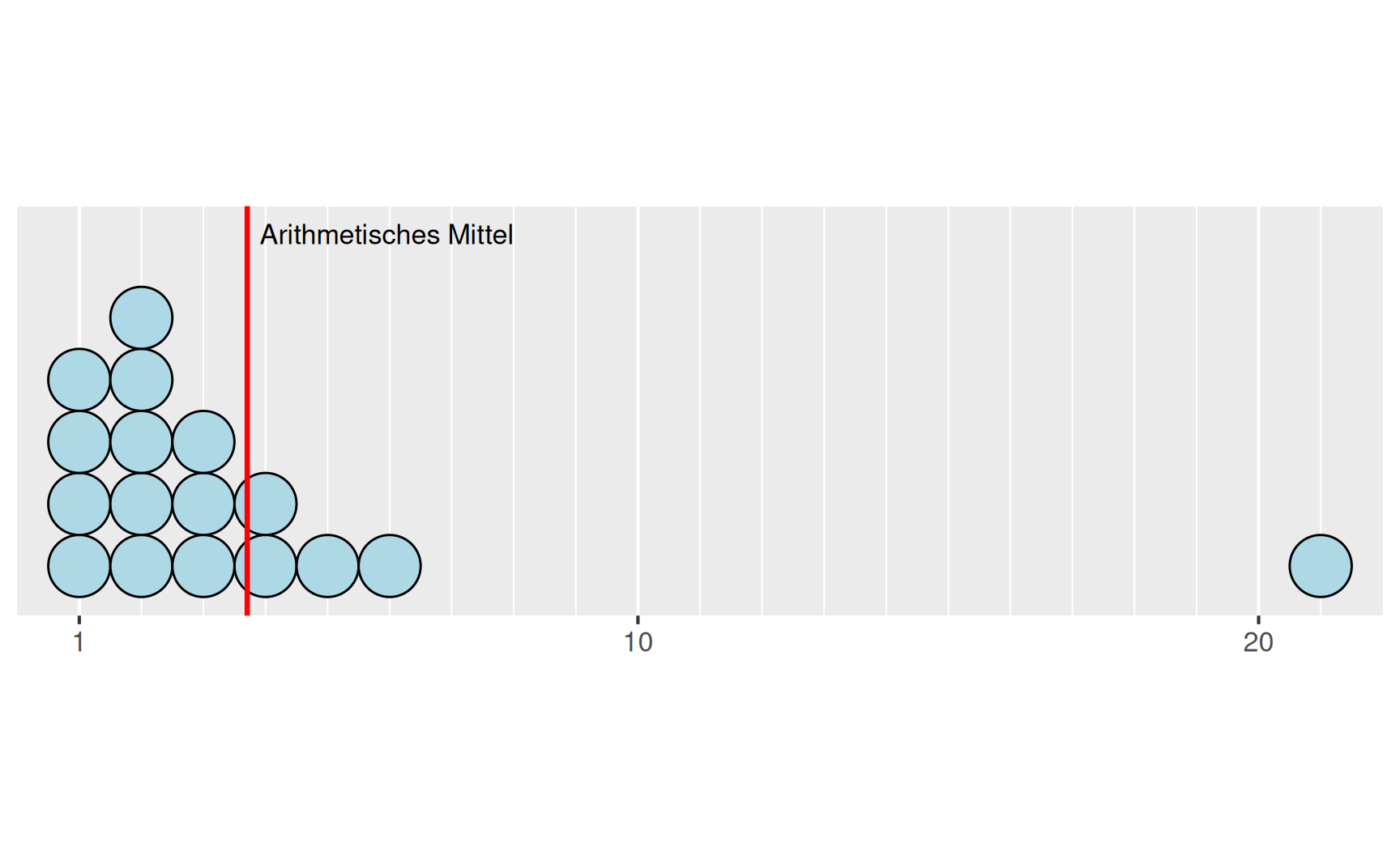
Arithmetisches Mittel von Merkmal \(Y\) \[ \bar{y} = \frac{1}{17}(1 + 2 + 6 + \dots + 21 + \dots + 2) = 3.705\dots \]
Wir sehen, dass sich der Wert \(y_{13} = 21\) für das arithmetische Mittel \(\overline{y}\) offensichtlich stark auswirkt. Anhand der beiden oben festgehaltenen Eigenschaften des arithmetischen Mittels lässt sich das auf zwei Arten verstehen:
1.Der Abstand \((21 - a)\) geht quadratisch in die zu minimierende Summe ein
2.Der Hebelarm der Kugel zum Wert \(y_{13} = 21\) ist vergleichsweise groß
Für den Wert \(y_{13} = 21\) könnte man vermuten, dass es sich um einen Eingabefehler handelt: Es wurden aus Versehen die nebeneinanderliegenden Tasten 2 und 1 anstatt nur der Taste 2 gedrückt. In diesem Fall verzerrt der einzelne falsche Wert den Mittelwert stark.
Ausreißer. Der Wert \(y_{13} = 21\) in Beispiel Arithmetisches Mittel fällt aus dem Wertebereich der anderen Beobachtungen heraus. Man spricht bei einer solchen extremen Beobachtung von einem Ausreißer. Bei solchen Ausreißern kann es sich um wichtige Informationen handeln. Genausogut können sie aber auch auf Grund von Übertragungsfehlern oder fehlerhaften Messungen vorkommen. Ob es sich bei einem Ausreißer um einen zwar extremen, aber doch richtigen Wert oder aber um eine fehlerhafte Größe handelt, ist im Einzelfall sorgfältig zu prüfen.
Über die Entdeckung des Ozonlochs kursiert folgende Geschichte: Vom Wettersateliten Nimbus 7 wurden seit November 1978 extrem geringe Ozonwerte über der Antarktis gemeldet. Allerdings wurden diese Werte bei der automatischen Auswertung der Daten als Messfehler ausgesondert und nicht weiter beachtet. Erst 1984 wurde von Forschungsstationen die Existenz des Ozonlochs durch Beobachtungen belegt. Daraufhin zeigte eine Neuauswertung der Satelitendaten das gesamte Ausmaß des Problems. Nach (Ludwig 2006). Anmerkung: In Wirklichkeit war es wohl komplizierter, siehe (Pukelsheim 1990).
Empfindliche und robuste Lagemaße. Das arithmetische Mittel ist ein Lagemaß, dass gegenüber Ausreißern sehr empfindlich ist: Einzelne fehlerhafte Werte können den Mittelwert stark verfälschen. Lagemaße hingegen, die wenig anfällig gegenüber Extremwerten sind, heißen resistent oder robust.
4.2 Median
Der Median ist ein solches robustes Lagemaß. Der Median wird (grob gesprochen) so platziert, dass die eine Hälfte der Daten unterhalb und die andere Hälfte der Daten oberhalb des Medians liegen.
Um den Median für die Urliste \(x_1, x_2, \dots, x_n\) formal zu definieren, sortieren wir zunächst die Werte der Größe nach. Es ergibt sich die geordnete Urliste \(x_{(1)}, x_{(2)}, \dots, x_{(n)}\). Dabei sollen die in Klammern gesetzten Indizes deutlich machen, dass nun
\[ x_{(1)} \leq x_{(2)} \leq \dots \leq x_{(i)} \leq \dots \leq x_{(n)} \]
gelten soll. Für eine ungerade Anzahl an Beobachtungen ist der Median \(x_{med}\) nun der Wert, der in der geordneten Urliste in der Mitte steht; ist die Anzahl ungerade, dann ist es der Mittelwert der beiden in der Mitte stehenden Werte. Entsprechend definieren wir den Median für mindestens intervallskalierte Merkmale.
Definition (Median):
\[ x_{med} = \begin{cases} \;\; x_{\left(\frac{n+1}{2}\right)} & \text{für ungerades $n$} \\[1em] \;\; \frac{1}{2}\left(x_{(n/2)} + x_{(n/2+1)}\right) & \text{für gerades $n$} \end{cases} \]
Anders als das arithmetische Mittel kann der Median auch für ordinal skalierte Merkmale angegeben werden. Bei einer geraden Anzahl von Stichproben liegt der Median dann gegebenenfalls zwischen zwei Ausprägungen.
Darüber hinaus besitzt der Median \(x_{med}\) folgende Eigenschaften:
1.Der Median minimiert die Summe der Beträge der Abstände: \[x_{med}= \underset{a}{\operatorname{argmin}} \sum_{j=1}^n |x_j - a|\]
2.Mindestens 50% der Daten sind kleiner oder gleich dem Median \(x_{med}\) und mindestens 50% der Daten sind größer oder gleich dem Median \(x_{med}\).
An der ersten Eigenschaft ist nochmals zu erkennen, dass der Median im Vergleich zum arithmetischen Mittel ein resistentes Lagemaß darstellt: In den Betrag des Modus geht eine extrem große Abweichung vom Mittelwert wesentlich weniger stark ein als in das Quadrat des arithmetischen Mittels.
Beispiel Güteklasse:
Die Auswertung eines Merkmals “Güteklasse” ergab die Liste
| Beobachtung | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Urliste | A | A | C | A | B | B | D | B | C | A | B | D |
| geordnete Urliste | A | A | A | A | B | B | B | B | C | C | D | D |
mit dem Umfang \(n = 12\). Der Median liegt daher zwischen \(x_{6} = \text{B}\) und \(x_{7} = \text{B}\). Beide Werte sind gleich, also ist \(x_{med} = \text{B}\).
4.3 Modus
Ein weiteres Lagemaß ist der Modus, der angibt, welche Ausprägung am häufigsten vorkommt.
Definition (Modus):
Der Modus \(x_{mod}\) ist diejenige Ausprägung eines Merkmals, die am häufigsten vorkommt. Der Modus ist nur dann eindeutig bestimmt, wenn die Verteilung ein eindeutiges Maximum besitzt.
Der Modus lässt sich für alle Arten von Merkmalen bestimmen, auch wenn es sich nur um eine nominalskalierte Größe handelt. In der Darstellung durch ein Stab- oder Säulendiagramm entspricht der Modus der Ausprägung mit dem höchsten Stab bzw. der höchsten Säule.
4.4 Lageregeln
Falls es sich um eine unimodale Verteilung handelt, kann aus den Zahlenwerten von arithmetischem Mittel, Median und Modus auf die Schiefe der Verteilung geschlossen werden. Hierzu zunächst ein Beispiel (aus (Fahrmeir u. a. 2016)).
Wir betrachten drei Verteilungen, für die bereits die drei oben besprochenen Lagemaße bestimmt wurden.
| \(a_i\) | Stichprobe I \(h(a_i)\) |
Stichprobe II \(h(a_i)\) |
Stichprobe III \(h(a_i)\) |
|---|---|---|---|
| 1 | 8 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 8 | 4 | 2 |
| 4 | 6 | 8 | 4 |
| 5 | 5 | 10 | 5 |
| 6 | 4 | 8 | 6 |
| 7 | 2 | 4 | 8 |
| 8 | 2 | 2 | 10 |
| 9 | 1 | 1 | 8 |
| \(\bar{x}\) | 3.57 | 5 | 6.43 |
| \(x_{med}\) | 3 | 5 | 7 |
| \(x_{mod}\) | 2 | 5 | 8 |
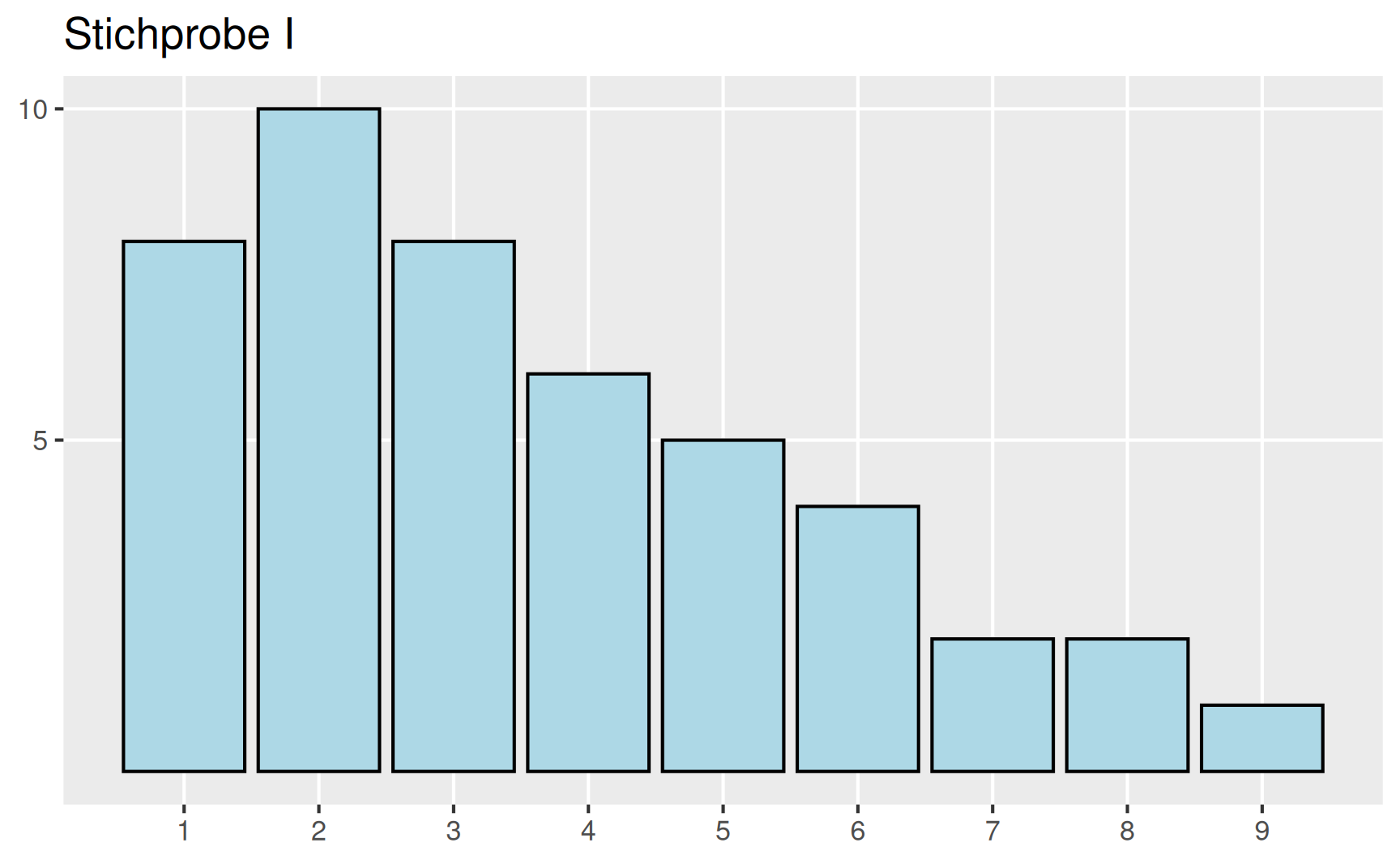
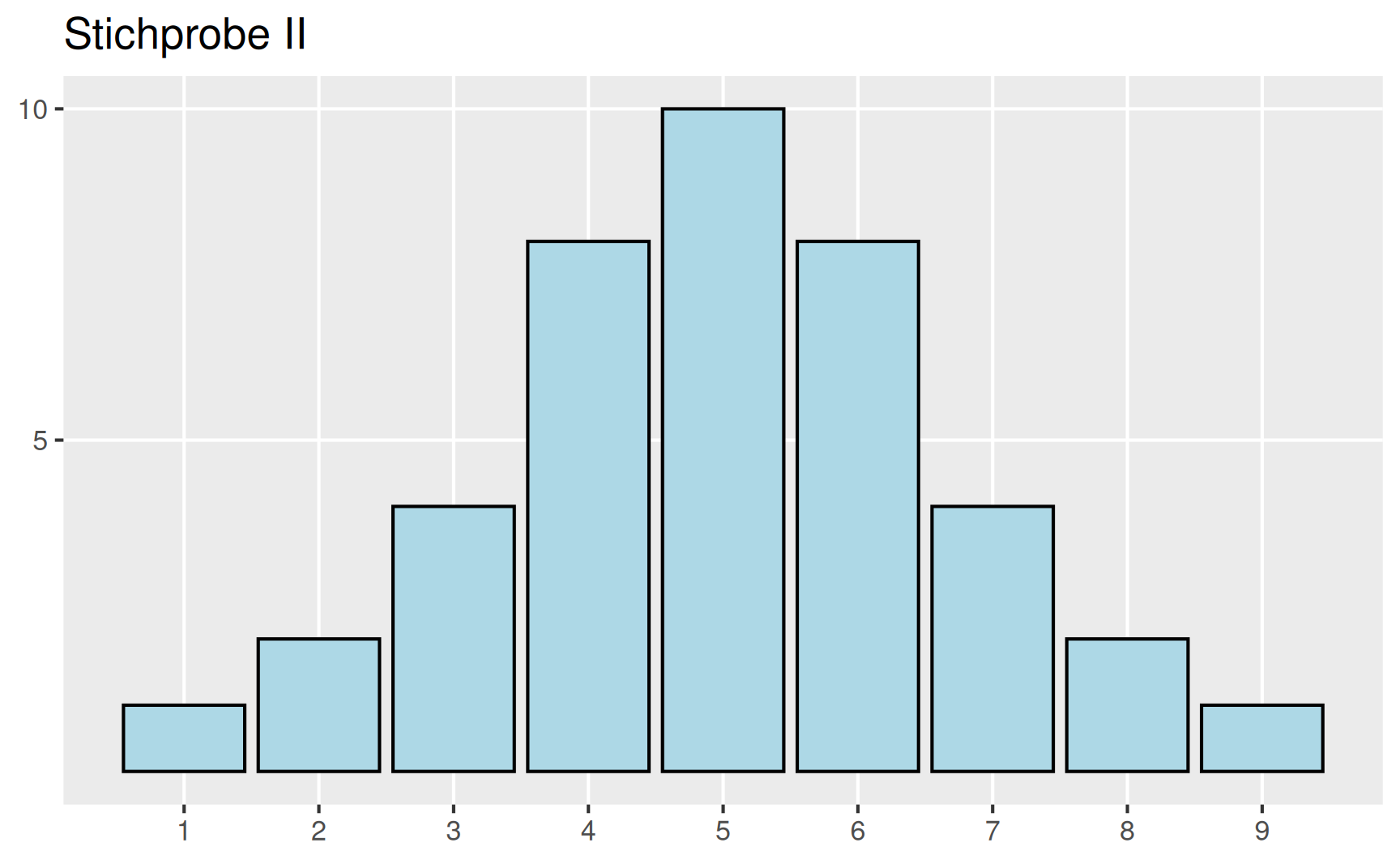
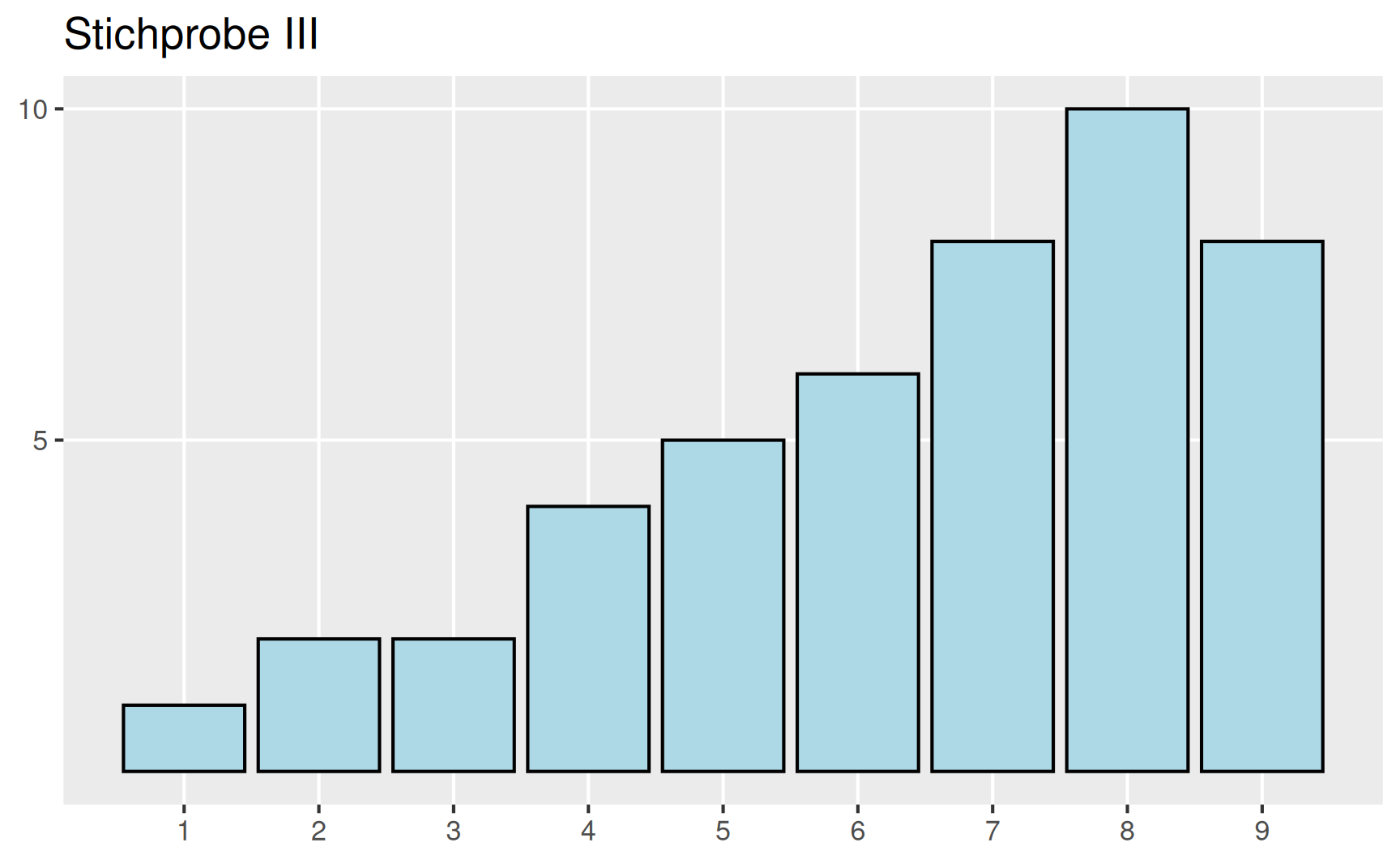
Offensichtlich besteht hier folgender Zusammenhang zischen der Form der Verteilung und den Größen der drei Lagemaße:
\[ \begin{aligned} \text{Stichprobe I} & \quad \text{linkssteil} & \quad \bar{x} > x_{med} > x_{mod} \\ \text{Stichprobe II} & \quad \text{symmetrisch} & \quad \bar{x} = x_{med} = x_{mod} \\ \text {Stichprobe III} & \quad \text{rechtssteil} & \quad \bar{x} < x_{med} < x_{mod} \end{aligned} \]
Außerdem halten wir fest, dass alle Verteilungen unimodal sind.
Muss der im Beispiel beobachtete Zusammenhang zwischen Symmetrie und Steilheit und den Größen der Lagemaße immer gelten? Wir überlegen uns hierzu:
Für eine schiefe Verteilung zieht der “Hebelarm’’ der flach auslaufenden kleineren Werte das arithmetische Mittel in die Richtung der Schiefe.
Es lässt sich zeigen, dass auf der steilen Seite des Modus weniger als die Hälfte der Werte angesiedelt sind. Der Median liegt daher bei einer schiefen Verteilung zwischen Modus und arithmetischem Mittel.
Bei einer symmetrischen Verteilung liegt der höchste Punkt in der Mitte, ebenso das arithmetisches Mittel sowie der Median. Allerdings sind reale Verteilungen selten exakt symmetrisch, so dass wir nur die ungefähre Gleichheit der drei Lagemaße fordern können.
Wir halten also die Lageregeln
Definition (Lageregeln): Für eine unimodale Verteilung gilt
\[ \begin{aligned} \text{Linkssteil} \quad \iff \bar{x} > x_{med} > x_{mod} \\ \text{Symmetrisch} \quad \iff \bar{x} \approx x_{med} \approx x_{mod} \\ \text{Rechtssteil} \quad \iff \bar{x} < x_{med} < x_{mod} \end{aligned} \]
fest. Beachten Sie dabei, dass die Verwendung der Begriffe unimodal, linkssteil, symmetrisch und rechtssteil immer einen gewissen Ermessensspielraum beinhaltet und die Lageregeln daher in erster Linie als Interpretationshilfen zu verstehen sind.
4.5 Das geometrische Mittel
Das geometrische Mittel wird verwendet, wenn es sich bei den Werten eines Merkmals um Wachstumsfaktoren handelt.
Beispiel Wasserreservoir
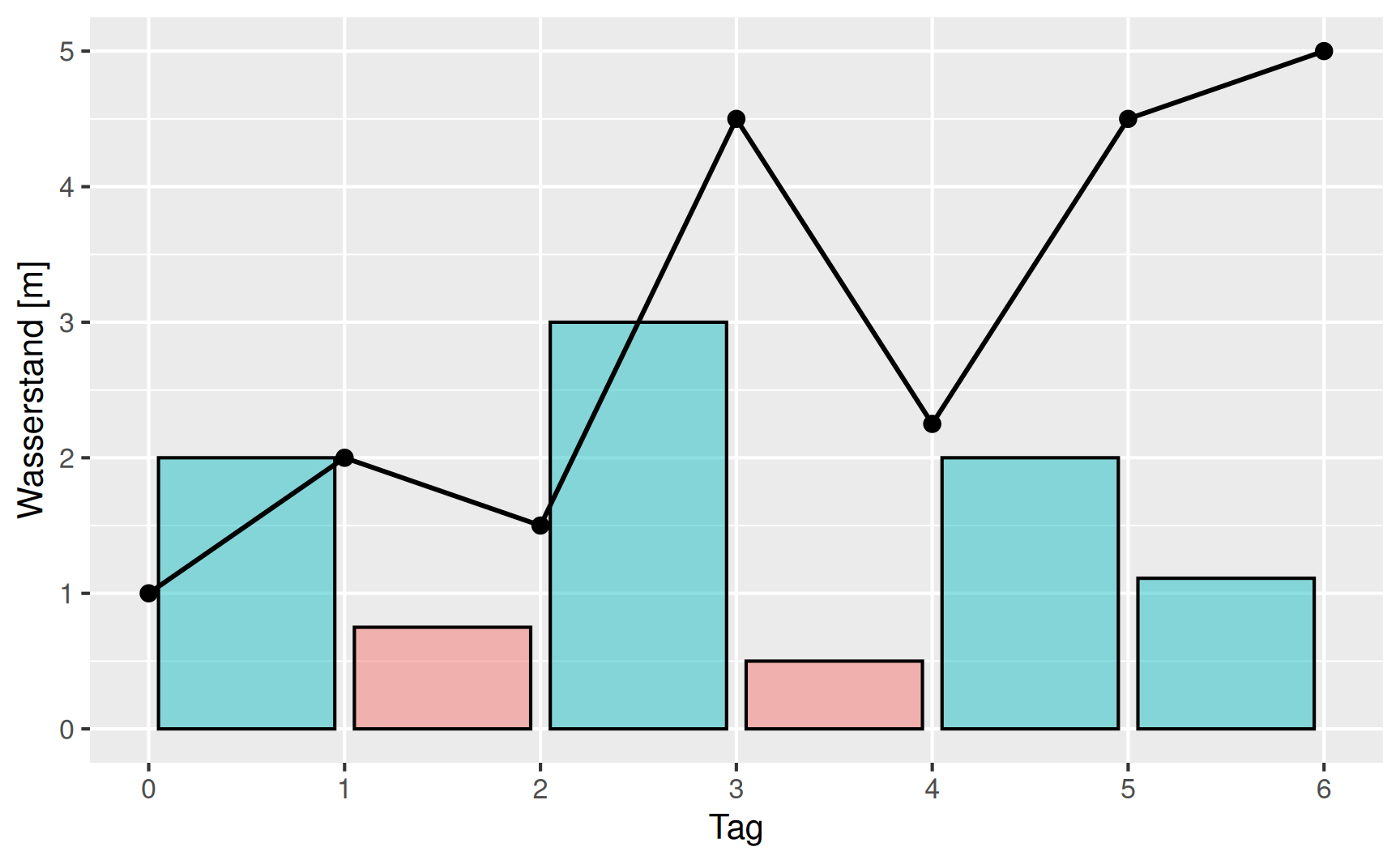
Wir betrachten ein Wasserreservoir mit den Wasserständen
| Tag \(i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Wasserstand \(W_i\) | 1.00 | 2.00 | 1.50 | 4.50 | 2.25 | 4.50 | 5.00 |
Dann ist für jeden Zeitraum \(i = 1, \dots, n\) das Verhältnis der beiden Wasserstände
\[ x_i = W_i / W_{i-i} \]
der \(i\)-te Wachstumsfaktor. Insgesamt ergeben sich für den Wachstumsfaktor die Werte
| Zeitraum \(i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| Wachstumsfaktor \(x_i\) | 2.00 | 0.75 | 3.00 | 0.50 | 2.00 | \(1.\overline{1}\) |
Grafisch stellt sich die Situation so dar:
Aus der Definition des Wachstumsfaktors erhalten wir \(W_i = x_i W_{j-i}\). Mit den Wachstumsfaktoren \(x_i\) und dem Wasserstand \(W_0 = 1\) können wir also den Verlauf des Wasserstandes für die betrachteten Tage rekonstruieren:
\[ W_1 = x_1 \cdot W_0 = 2 \cdot 1 = 2 \quad = x_1 \cdot W_0 \]
\[ W_2 = x_2 \cdot W_1 = 0.75 \cdot 2 = 1.5 \quad = x_2 \cdot x_1 \cdot W_0 \]
\[ W_3 = x_3 \cdot W_2 = 3.00 \cdot 1.5 = 4.5 \quad = x_3 \cdot x_2 \cdot x_1 \cdot W_0 \]
\[ \vdots \]
\[ W_6 = x_6 \cdot W_5 = 1.\overline{1} \cdot 4.5 = 5 \quad = x_6 \cdot x_5 \cdot x_4 \cdot x_3 \cdot x_2 \cdot x_1 \cdot W_0 \]
Für einen mittleren Wachstumsfaktor \(z\) müssen wir dasselbe Ergebnis erhalten, wenn wir sechs Tage lang diesen Wachstumsfaktor ansetzen. Es muss gelten
\[ W_6 = z \cdot z \cdot z \cdot z \cdot z \cdot z \cdot W_0 = z^6 \cdot W_0 \]
so dass wir den mittleren Wachstumsfaktor
\[ z = \sqrt[6]{x_6 \cdot x_5 \cdot x_4 \cdot x_3 \cdot x_2 \cdot x_1} = \sqrt[6]{ 2.00 \cdot 0.75 \cdot 3.00 \cdot 0.50 \cdot 2.00 \cdot 1.\overline{1}}= \sqrt[6]{5} = 1.307\dots \]
für den Wasserstand erhalten.
Hier nochmals die Situation mit dem mittleren Wachstum.
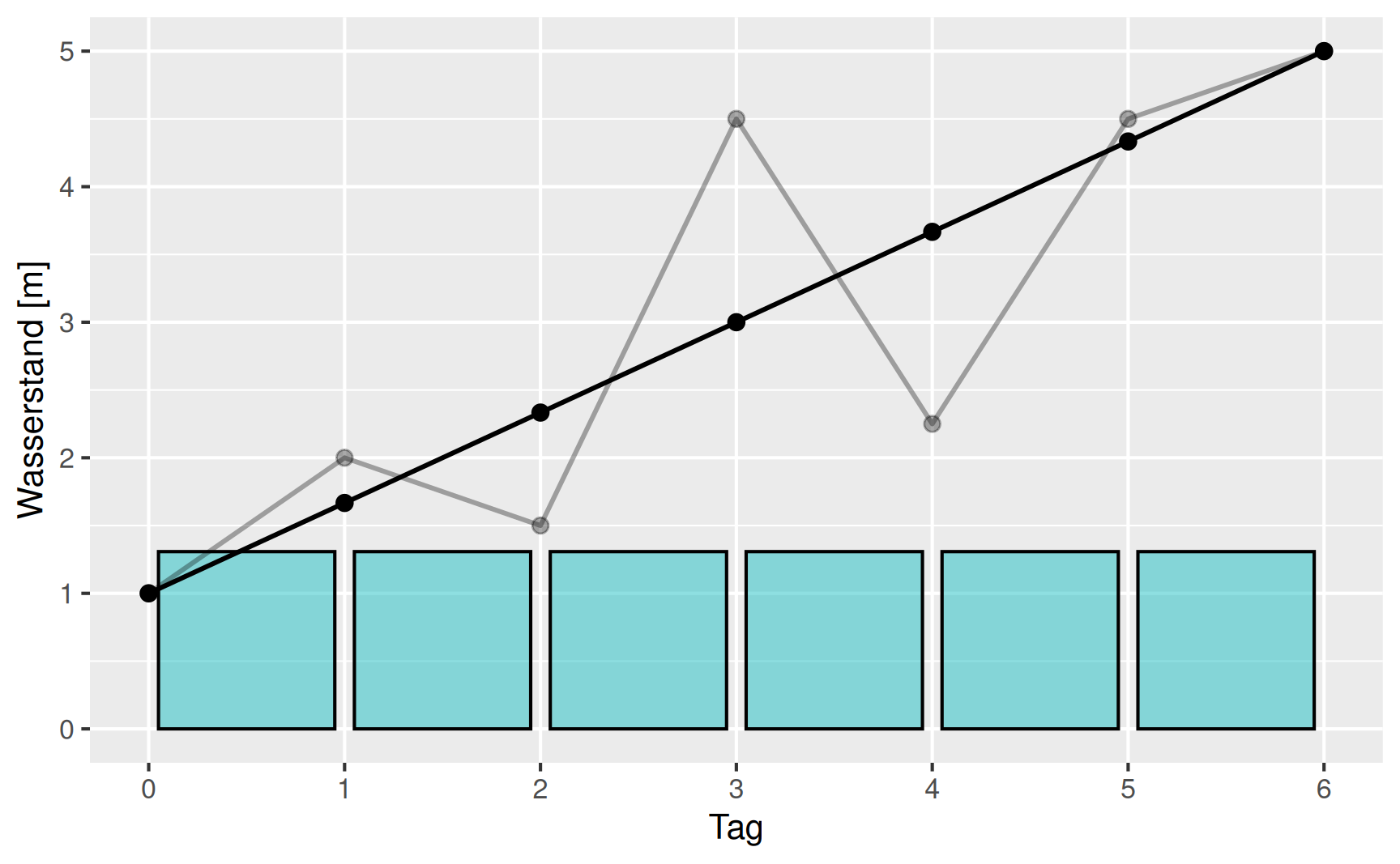
Entsprechend der Überlegung im Beispiel definieren wir
Definition (Geometrisches Mittel): Das geometrische Mittel zu den Faktoren \(x_1, x_2, \dots, x_n\) ist die \(n\)-te Wurzel aus dem Produkt der Faktoren, also \[ \bar{x}_{geom} = (x_1 \cdot x_2 \cdot \dots \cdot x_n)^{1/n}. \]
Daraus erhält man für einen Bestand \(B_0, B_1, \dots, B_n\) mit den Wachstumsfaktoren \(x_i = B_i / B_{i-1}, \quad i = 1, \dots, n\) den Zusammenhang
\[ B_n = \underbrace{\bar{x}_{geom} \cdot \; \dots \; \cdot \bar{x}_{geom}}_{n-\mathrm{mal}} \cdot B_0 = (\bar{x}_{geom})^n B_0. \]
Mit \(\bar{x}_{geom}\) als mittlerem Wachstumsfaktor für alle Perioden ermittelt man also denselben Bestand \(B_n\), der sich auch mit den tatsächlichen Wachstumsfaktoren \(x_1, \dots, x_n\) ergibt. In diesem Sinn ist \(\bar{x}_{geom}\) die adäquate Mittelung der Wachstumsfaktoren.
4.6 Das harmonische Mittel
Als letztes Lagemaß betrachten wir das harmonische Mittel. Es wird verwendet, wenn das zu mittelnde Merkmal eine Verhältnisgröße ist, bei der die Häufigkeit im Zähler steht. Beispiele sind die Geschwindigkeit (Weg/Zeit) oder die Dichte (Masse/Volumen).
Beispiel Autofahrt:
Bei einer Autofahrt werden zunächst 10km mit einer Geschwindigkeit von 50km/h zurückgelegt, danach weitere 60km bei 110km/h. Wie groß ist die Durchschnittsgeschwindigkeit?
Zunächst bestimmen wir die Gesamtstrecke und die gesamte Fahrzeit:
\[ S = 10 + 60 = 70 km \quad \text{und} \quad T = 10 \cdot 1 / 50 + 60 \cdot 1 / 110 \approx 0.7455\ h \]
und somit die Durchschnittsgeschwindigkeit
\[ 70 / 0.7455 = 93.9 \, km/h. \]
Verallgemeinerungsfähig wird das dann, wenn wir die Situation etwas anders formulieren: Es liegen für die Fahrstrecke 70 Beobachtungen über die Geschwindigkeit vor, eine für jeden gefahrenen Kilometer. Dabei entsprechen 10 Beobachtungen einem Wert von 50km/h und 60 einem Wert von 110km/h. Damit entspricht die Durchschnittsgeschwindigkeit dem Bruch
\[ \frac{70}{ \displaystyle \underbrace{\frac{1}{50} + \dots + \frac{1}{50}}_{10 - \mathrm{mal}} + \underbrace{\frac{1}{110} + \dots + \frac{1}{110}}_{60 - \mathrm{mal}} } \]
Wir haben damit die Definition des harmonischen Mittels gefunden.
Definition (Harmonisches Mittel): Für die Werte \(x_1, \dots, x_n\) heißt die Zahl
\[ \bar{x}_{har} = \frac{n}{\displaystyle \sum_{i=1}^n\frac{1}{x_i}} \] harmonisches Mittel.
5 Maße der Variabilität
Mit den verschiedenen Lagemaßen lässt sich die ungefähre Lage der Werte auf dem Zahlenstrahl angeben. Allerdings können zwei sehr unterschiedliche Stichproben ein und dasselbe Lagemaß aufweisen. Wir überlegen uns nun, wie wir die Variabilität eines Merkmals messen können.
Welche Eigenschaften soll nun ein solches Variabilitätsmaß haben? Es ist naheliegend zu erwarten, dass wir eine Variabilität von Null erhalten, wenn alle betrachteten Werte identisch sind. Demzufolge wächst die Zahl mit zunehmender Variabilität an, so dass eine negative Variabilität keinen Sinn ergibt. Darüber hinaus soll das Maß für die Variabilität nicht vom Umfang der Stichprobe abhängen.
Im Jahr 2010 titelte der Spiegel “So verrückt war dieser Sommer”: Noch nie hat es seit Beginn der Aufzeichnungen 1881 im August so viel geregnet.


Die Bilder links (Quelle: spiegel.de) zeigen, wie sich das extreme Wetter des Jahres 2010 in Dresden auswirkte. Die Elbe führt im Juli fast kein Wasser, nur um kurz darauf im August über die Ufer zu treten.
Wie war es in diesem Jahr 2010 in Bochum und wie verhält es sich im Vergleich dazu in einem “normalen’’ Jahr? Wir betrachten hierzu die Monatssumme der täglichen Niederschlagshöhe in Bochum für die Jahre 2008 und 2010 (Quelle: Deutscher Wetterdienst). Die Werte sind in Millimetern angegeben.
| Jahr | Jan | Feb | Mär | Apr | Mai | Jun | Jul | Aug | Sep | Okt | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 91.8 | 48.9 | 76.3 | 67.3 | 45.8 | 62.7 | 114.7 | 101.4 | 77.7 | 78.9 | 60.0 | 43.9 |
| 2010 | 48.6 | 73.0 | 68.0 | 11.4 | 52.0 | 22.6 | 78.7 | 187.4 | 72.3 | 51.2 | 126.6 | 84.8 |
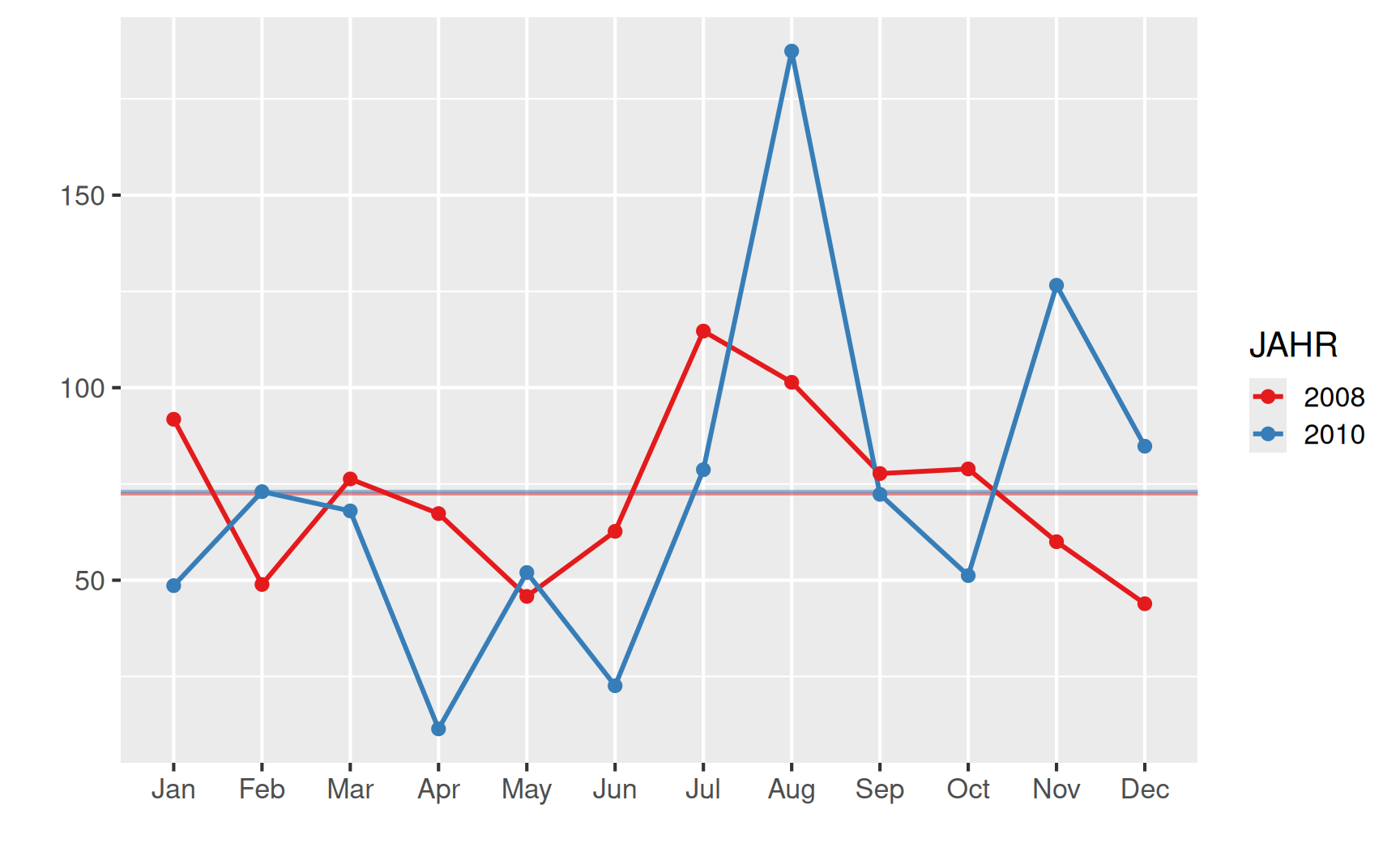
Trotz des extremem Wetters im Jahr 2010 liegen die arithmetischen Mittelwerte der Niederschläge in beiden Jahren mit
\[ \bar{x}_{2008} = \frac{1}{12}(91.8 + 48.9 + \cdots + 43.9) = 72.45\ mm \]
\[ \bar{x}_{2010} = \frac{1}{12}(48.6 + 73.0 + \cdots + 84.8) = 73.05\ mm \]
sehr nah beieinander (horizontale Linien im Plot). In der Summe hat es in beiden Jahren ungefähr gleich viel geregnet. Allerdings waren 2010 die Monate April und Juni sehr trocken, während es im August extrem viel geregnet hat. Im Vergleich dazu liegen die monatlichen Werte im Jahr 2008 insgesamt deutlich näher am Mittelwert.
Derartige Zusammenhänge versucht man mithilfe von Streuungsmaßen zu erfassen.
Spannweite.
Das einfachste Streuungsmaß ist die Spannweite \(R\) eines Merkmals(englisch: range), die angibt, wie weit der größte und der kleinste Wert auseinanderliegen:
\[ R = \max x_i - \min x_i. \] Die Spannweite ist zwar einfach zu berechnen, allerdings hat sie den Nachteil, dass sie allein von zwei Werten abhängt und daher kein robustes Maß darstellt.
Für die Niederschläge der Jahre 2008 und 2010 betragen die Spannweiten der monatlichen Mittelwerte
\[ R_{2008} = 114.7 - 43.9 = 70.8mm \quad \text{und} \quad R_{2010} = 187.4 - 11.4 = 176.0mm. \]
Sie unterscheiden sich also deutlich.
AD-Streuung, Varianz und Standardabweichung.
Um zu einem robusteren Maß für die Variabilität der Daten zu gelangen, müssen wir alle Werte in die Berechnung einbeziehen. Als Grundlage hierfür dient die Abweichung der einzelnen Beobachtungen vom arithmetischen Mittel, also die Zahlenwerte \((x_i - \bar{x}), \;\; i = 1, \dots, n\). Streuungsmaße auf Basis des Medians sind nicht üblich.
Für die Situation in Bochum bestimmen wir also zunächst die Abweichungen der monatlichen Niederschläge vom Mittelwert.
| Jahr | Jan | Feb | Mär | Apr | Mai | Jun | Jul | Aug | Sep | Okt | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 19.35 | -23.55 | 3.85 | -5.15 | -26.65 | -9.75 | 42.25 | 28.95 | 5.25 | 6.45 | -12.45 | -28.55 |
| 2010 | -24.45 | -0.05 | -5.05 | -61.65 | -21.05 | -50.45 | 5.65 | 114.35 | -0.75 | -21.85 | 53.55 | 11.75 |
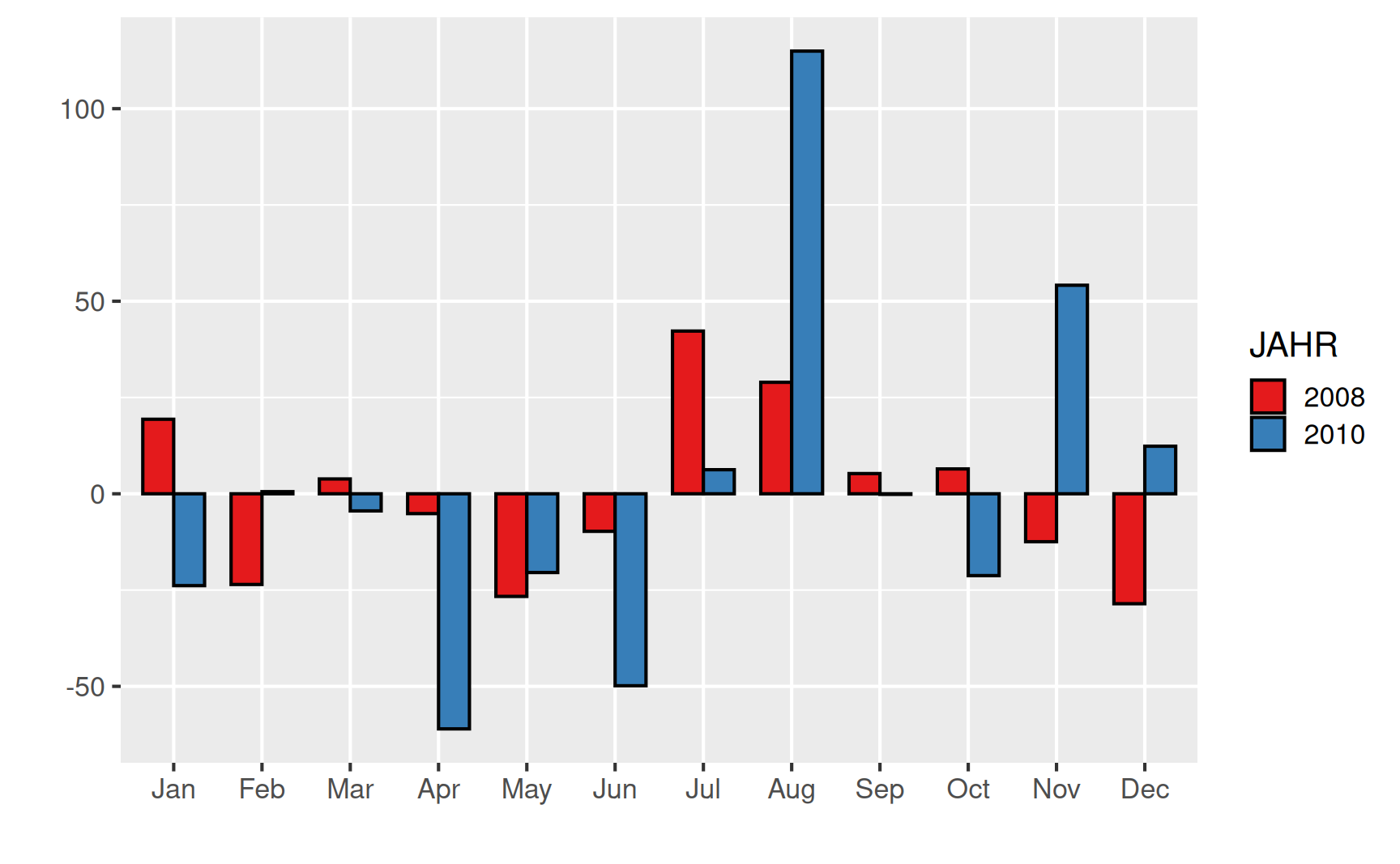
Man könnte nun auf die Idee kommen, die Abweichungen \((x_i - \bar{x})\) einfach aufzuaddieren. Eine kurze Überschlagsrechung im Kopf zeigt jedoch für unser Beispiel, dass die Summen für beide Jahre nahe bei Null liegen. Dass sie sogar exakt null sein müssen, wird sofort klar, wenn man sich überlegt, was da eigentlich addiert wird:
\[ \sum_{i=1}^n(x_i - \bar{x}) = \sum_{i=1}^n x_i - n \cdot \bar{x} = n\bigg(\underbrace{\frac{1}{n}\sum_{i=1}^n x_i}_{\bar{x}} - \bar{x}_{mid} \bigg) = 0. \]
Die Summe der Abweichungen vom Mittelwert ist also keinesfalls ein geeignetes Maß für Variabilität.
Das Problem der sich aufhebenden Summanden lässt sich natürlich dadurch umgehen, dass wir die Beträge der Abweichungen \(x_i - \bar{x}\) addieren. Wir erhalten damit die AD-Streuung average deviation
\[ AD = \frac{1}{n} \left( |x_1 - \bar{x}| + \dots + |x_n - \bar{x}| \right) = \frac{1}{n} \cdot \sum_{i=1}^n |x_i - \bar{x}| \]
mit den gewünschten Eigenschaften. Allerdings sind die Betragsstriche in der Handhabung umständlich, zum Beispiel wenn Ableitungen berechnet werden sollen (Fallunterscheidung!). Die AD-Streuung wird daher nur äußerst selten verwendet.
Eine weitere Möglichkeit besteht darin, die Summanden \(x_i - \bar{x}\) zu quadrieren um sicherzustellen, dass nur positive Zahlen aufsummiert werden. Dieser Gedanke führt uns auf die empirische Varianz
\[ \tilde{s}^2 = \frac{1}{n} \left( (x_1 - \bar{x})^2 + \dots + (x_n - \bar{x})^2 \right) = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \bar{x})^2. \]
Die Varianz ist also das arithmetische Mittel der quadrierten Abweichungen. Sie ist klein, wenn die Werte nahe des Mittelwerts angesiedelt sind. Infolge des Quadrierens hat \(\tilde{s}^2\) nicht die gleiche Maßeinheit wie die Werte \(x_i\).
Schließlich kann man aus der Summe der quadrierten Abweichungen noch die Wurzel ziehen. Der Wert
\[ \tilde{s} = \sqrt{\tilde{s}^2} = \sqrt{\frac{1}{n} \cdot \sum_{i=1}^n (x_i - \bar{x})^2} \]
heißt empirische Standardabweichung. Die Einheit der Standardabweichung stimmt wieder mit der Einheit des Merkmals überein.
Für die Niederschläge in den Jahren 2008 und 2010 in Bochum erhalten wir die empirischen Varianzen
\[ \tilde{s}^2_{2008} = \frac{1}{12}\left((19.35)^2 + (-23.55)^2 + \dots + (-28.55)^2 \right) \approx 453.17mm^2 \]
\[ \tilde{s}^2_{2010} = \frac{1}{12}\left( (-24.45)^2 + (-0.05)^2 + \dots + (11.75)^2 \right) \approx 2000.32mm^2 \]
sowie die Standardabweichungen
\[ \tilde{s}_{2008} = \sqrt{453.17} = 21.29mm \quad \text{und} \quad \tilde{s}_{2010} = \sqrt{2000.32} = 44.7mm. \]
Die unterschiedliche Niederschlagscharakteristik der beiden Jahre kommt in diesen Streuungsmaßen deutlich zum Ausdruck. Die Standardabweichung ist dabei einfacher zu interpretieren, da sie im selben Wertebereich wie die Beobachtungen selber liegen.
In der schließenden Statistik wird die empirische Varianz in einer leicht veränderten Form verwendet: Man dividiert durch \(n-1\) und erhält die Stichprobenvarianz
\[ s^2 = \frac{1}{n - 1} \cdot \sum_{i=1}^n (x_i - \bar{x})^2, \]
auf die im entsprechenden Kapitel genauer eingegangen wird. Für größere Werte von \(n\) ist der Unterschied zwischen \(\tilde{s}^2\) und \(s^2\) vernachlässigbar.
Variationskoeffizient. Für ein Merkmal mit nichtnegativen Ausprägungen und einem Mittelwert \(\bar{x} > 0\) kann die Standardabweichung noch auf den Mittelwert bezogen werden. Man erhält den dimensionslosen Variationskoeffizienten
\[ v = \frac{\tilde{s}}{\bar{x}}, \]
der angibt, wie groß die Variabilität im Verhältnis zum Mittelwert ist.
Für die Niederschlagsmengen erhalten wir
\[ v_{2008} \approx \frac{21.29}{72.45} \approx 0.29 \quad \text{und} \quad v_{2010} \approx \frac{44.72}{73.05} \approx 0.61. \]
Streuungsmaße
\[ \begin{aligned} R = \max x_i - \min x_i &: \text{Spannweite} \\ AD = \frac{1}{n} \cdot \sum_{i=1}^n |x_i - \bar{x}| &: \text{AD-Streuung} \\ \tilde{s}^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \bar{x})^2 &: \text{Empirische Varianz} \\ \tilde{s} = \sqrt{\tilde{s}^2} &: \text{Empirische Standardabweichung} \\ v = \frac{\tilde{s}}{\bar{x}} &: \text{Variationskoeffizient} \\ s^2 = \frac{1}{n - 1} \cdot \sum_{i=1}^n (x_i - \bar{x})^2 &: \text{Stichprobenvarianz} \\ \end{aligned} \]
6 Quantile und Box-Plots
Mit den Lage- und Variabilitätsmaßen haben wir nun die Möglichkeit eine Verteilung mithilfe von zwei Zahlen zusammenzufassen. Eine umfassendere, aber immer noch sehr kompakte Charakterisierung von Verteilungen erhält man, wenn zusätzlich die so genannten Quartilwerte hinzugenommen werden. Man erhält mit diesen Werten die Basis für die so genannte Fünf-Punkte-Zusammenfassung und den Box-Plot.
6.1 Quantile
Die oben genannten Quartile sind, wie auch der Median, spezielle Quantilwerte. Sie erinnern sich: Der Median \(x_{med}\) war so gewählt, dass die eine Hälfte (also 50%) der Werte kleiner gleich \(x_{med}\) sind und die andere Hälfte (also ebenfalls 50%) der Werte größer gleich \(x_{med}\). Für die Stichprobe mit 20 Werten
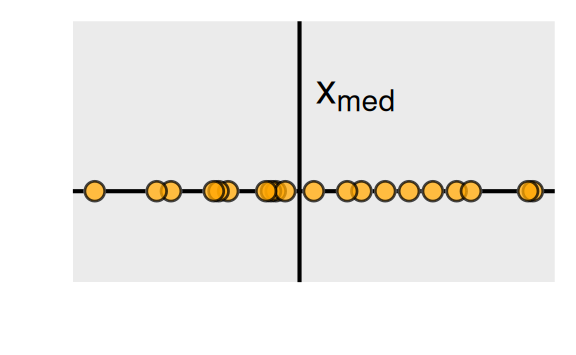
liegt der Median demnach in der Mitte zwischen dem zehnten und dem elften Wert.
Die Quantile verallgemeinern die Idee des Medians nun dahingehend, dass die Stichprobe in zwei unterschiedlich große Gruppen unterteilt wird. Das \(p\)-Quantil \(x_p\) (mit \(0 < p < 1\)) trennt die Daten so, dass \(p \cdot\) 100 % der Werte darunter und \((1 - p) \cdot\) 100% darüber liegen.
Für unsere zwanzig Werte können wir beispielhaft die Lage der folgenden \(p\)-Quantile bestimmen:
| \(p\) | Anzahl der Werte kleiner gleich \(x_p\) | Anzahl der Werte größer gleich \(x_p\) | Lage von \(x_p\) |
|---|---|---|---|
| 5% | \(0.05 \cdot 20 = 1\) | \((1 - 0.05)\cdot 20 = 19\) | zwischen \(x_{(1)}\) und \(x_{(2)}\) |
| 33% | \(0.33 \cdot 20 = 6.6\) | \((1 - 0.33)\cdot 20 = 13.4\) | bei \(x_{(7)}\) |
| 75% | \(0.75 \cdot 20 = 15\) | \((1 - 0.75)\cdot 20 = 5\) | zwischen \(x_{(15)}\) und \(x_{(16)}\) |
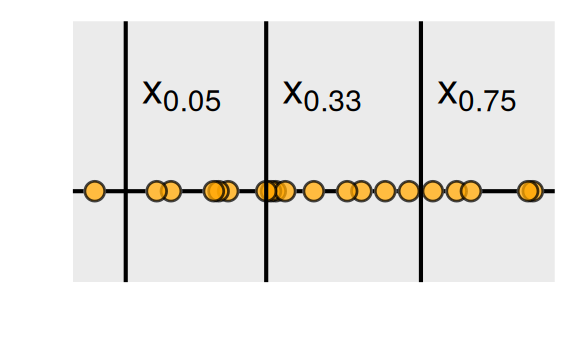
Wir sehen, dass wir die eingangs formulierte Idee noch etwas präzisieren müssen, um die Lage des Quantils eindeutig festlegen zu können.
Definition (Quantil): Eine Zahl \(x_p\) mit \(0 < p < 1\) heißt \(p\)-Quantil, wenn mindestens ein Anteil von \(p \cdot\) 100% der Daten kleiner/gleich \(x_p\) und mindestens ein Anteil von \((1-p) \cdot\) 100% größer/gleich \(x_p\) ist. Es muss für \(x_p\) also
\[ \frac{\text{Anzahl} (x\text{-Werte} \leq x_p)}{n} \geq p \quad \text{und} \quad \frac{\text{Anzahl} (x\text{-Werte} \geq x_p)}{n} \geq 1 - p \]
gelten. Fällt der Quantilwert zwischen zwei Werte, dann wird häufig (aber nicht immer) der Mittelwert verwendet. Damit erhalten wir mit der geordneten Urliste \(x_{(1)}, x_{(2)}, \dots, x_{(n)}\) für das Quantil \(x_p\) die Rechenvorschrift
\[ x_p = \begin{cases} x_{([pn]+1)} & \text{falls} \; p \cdot n \; \text{nicht ganzzahlig} \\[1em] \frac{1}{2} \cdot \left(x_{(pn)} + x_{(pn + 1)}\right) & \text{falls} \; p \cdot n \; \text{ganzzahlig} \end{cases}. \]
Dabei ist \([pn]\) die größte ganze Zahl, die kleiner als \(p \cdot n\) ist (runden nach unten).
Eine andere Möglichkeit, Quantile anschaulich zu interpretieren erhalten wir mithilfe der empirischen Verteilungsfunktion \(F\), die uns zu einer Zahl \(x\) sagt, welcher Anteil der Werte kleiner oder gleich \(x\) ist. Geben wir also ein \(p\)-Quantil vor, dann können wir den Wert \(x_p\) aus dem Graphen von \(F\) ablesen.
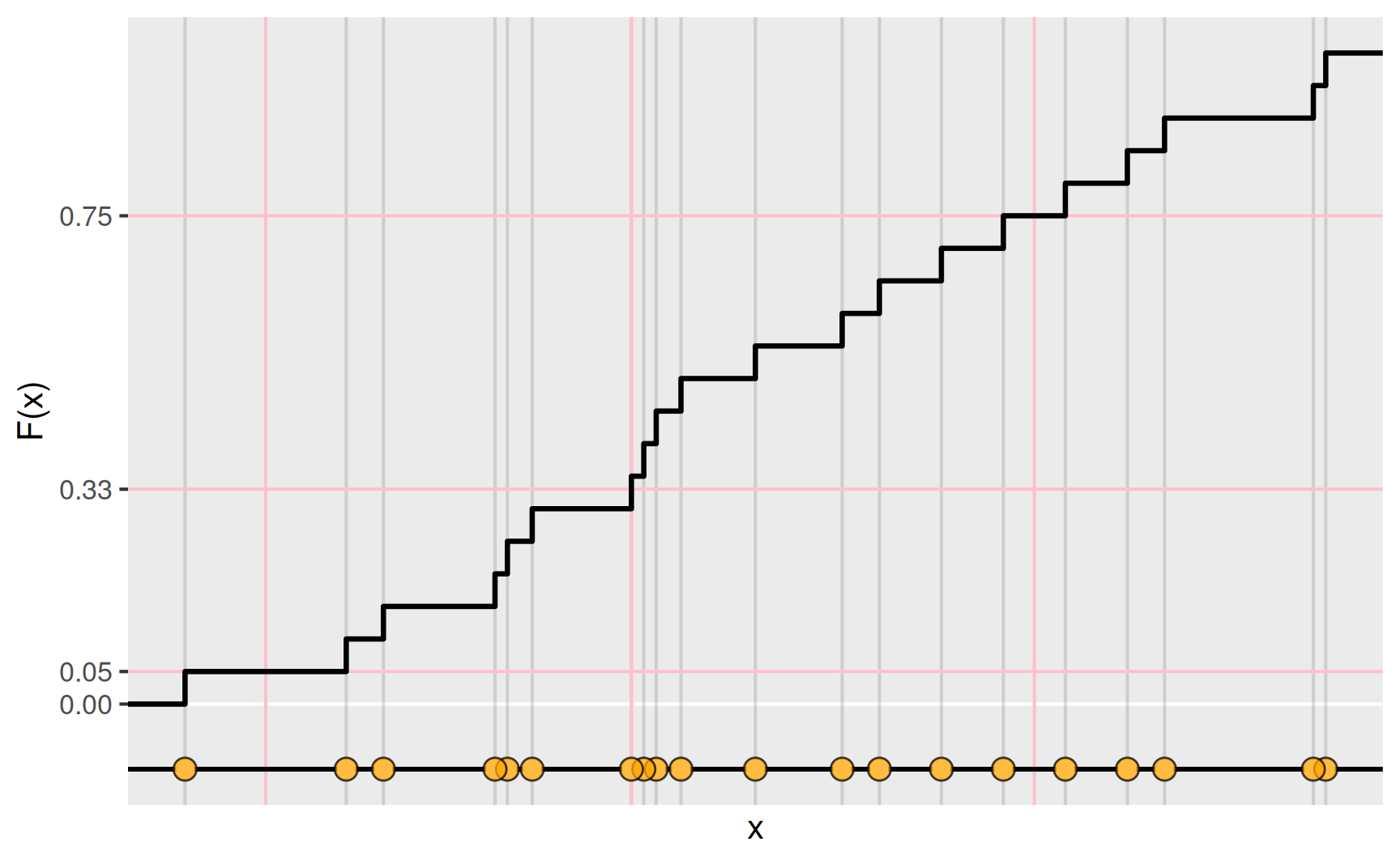
6.2 Quartile und Fünf-Punkte-Zusammenhang
Zwei bestimmte Quantilwerte werden immer wieder verwendet und haben daher eigene Namen:
- das 25%-Quantil \(x_{0.25}\) heißt unteres Quartil,
- das 75%-Quantil \(x_{0.75}\) heißt oberes Quartil.
Der Abstand zwischen diesen beiden Werten
\[d_{\mathrm{Q}} = x_{0.75} - x_{0.25}\]
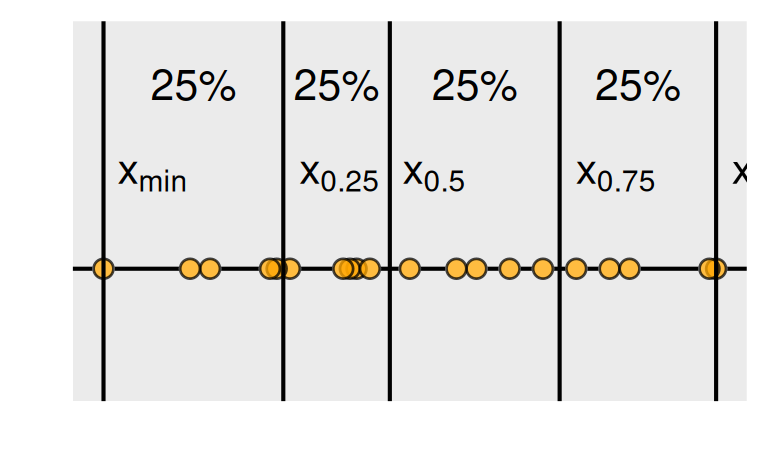
heißt Interquartilsabstand, kurz IQR (englisch: interquartile range). Zusammen mit den Extremwerten und dem Median erhalten wir die Fünf-Punkte-Zusammenfassung einer Verteilung
\[ x_{\mathrm{min}}, \; x_{0.25}, \; x_{med}, \; x_{0.75}, \; x_{\mathrm{max}}, \] mit der man die Verteilung in vier Bereiche aufteilt, die jeweils gleich viele Werte enthalten.
6.3 Box-Plot
Mit einem Box-Plot wird die Fünf-Punkte-Zusammenfassung graphisch dargestellt. Dabei wird unterschieden, ob es sich bei den Beobachtungen um ‘normale’ Werte oder um vermutete Ausreißer handelt. Der Boxplot ist eine komprimierte Zusammenfassung, an dem man einfach ablesen kann, wo die Verteilung liegt, wie stark sie streut und ob sie schief oder symmetrisch ist und ob es in dem Datensatz Ausreißer gibt.
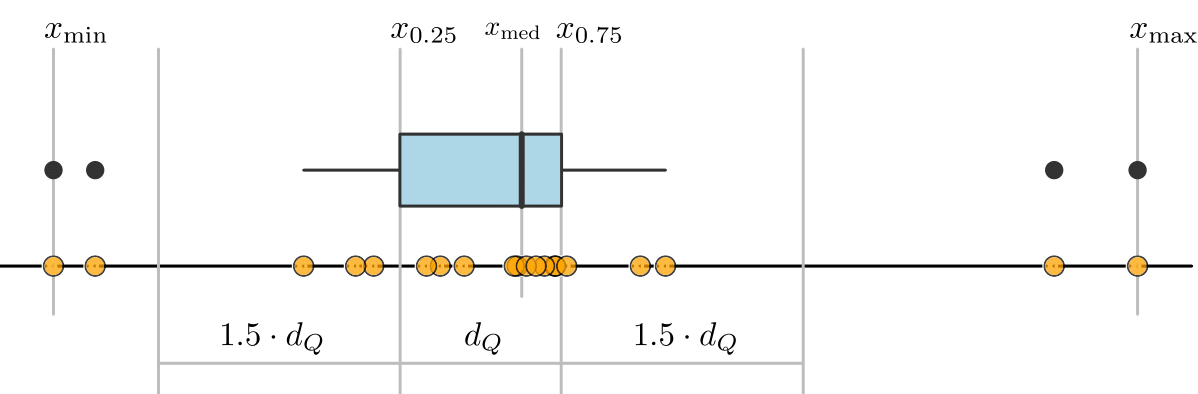
Ein Box-Plot entsteht in fünf Schritten:
- Ein Rechteck (englisch: box) liegt zwischen den Quartilen \(x_{0.25}\) und \(x_{0.75}\).
- Ein Strich in dem Rechteck markiert die Lage des Medians \(x_{med}\). 3.Alle Werte im Intervall \([x_{0.25} - 1.5 d_\mathrm{Q}, x_{0.75} + 1.5 d_\mathrm{Q}]\) werden als normale Beobachtungen angesehen.
- Zwei Linien (die whiskers) gehen bis zur kleinsten und bis zur größten normalen Beobachtung. Manchmal werden diese Linien durch einen kurzen Querstrich abgeschlossen.
- Alle Werte außerhalb des Intervalls der normalen Beobachtungen werden als Punkte eingezeichnet.
Die hier beschriebene Art von Box-Plots wird manchmal auch als modifizierter Box-Plot bezeichnet.
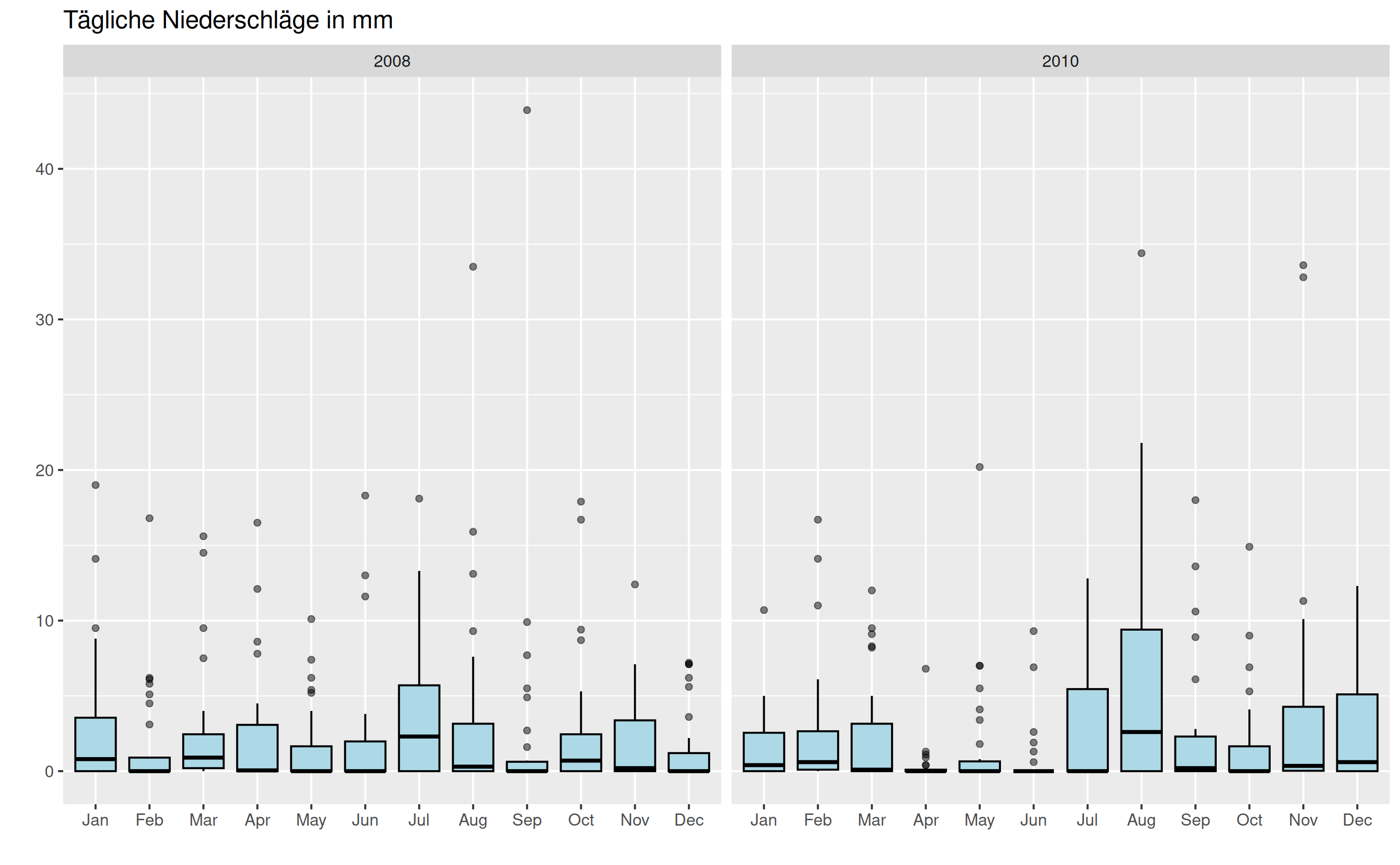
Unten dargestellt sind die Box-Plots der monatlichen Niederschläge in Bochum für die Jahre 2008 und 2010. Um zu verdeutlichen, wie die Box-Plots entstehen, sind seitlich jeweils noch die Niederschlagsmengen für die einzelnen Monate als Punkte dargestellt.
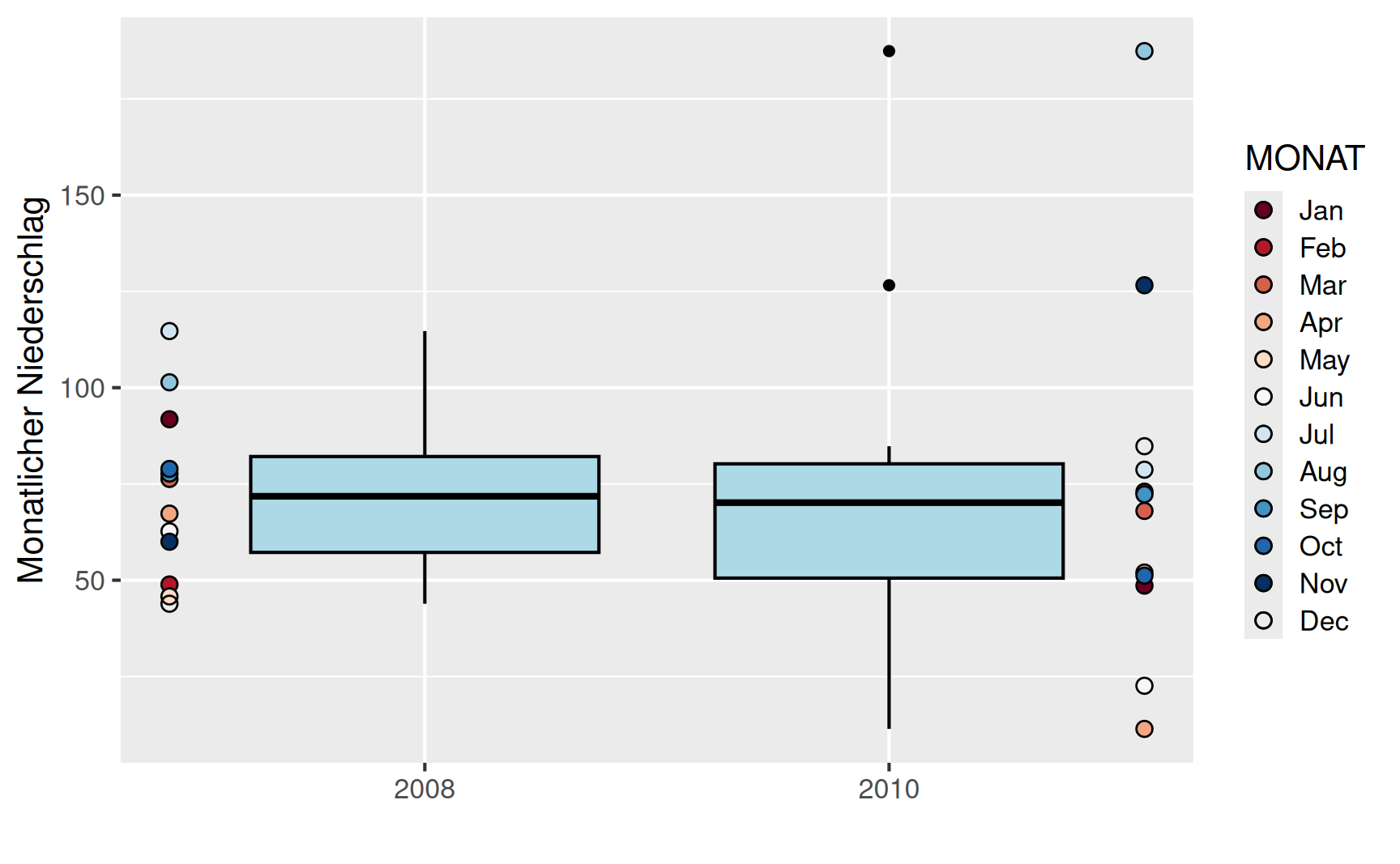
Einen genaueren Einblick in die Niederschläge der beiden Jahre erhalten wir auf Grundlage der täglichen Niederschläge. Die Charakteristik jedes Monats lässt sich dann wieder kompakt in einem Box-Plot zusammenfassen.
7 Konzentrationsmaß: Der Gini-Koeffizient
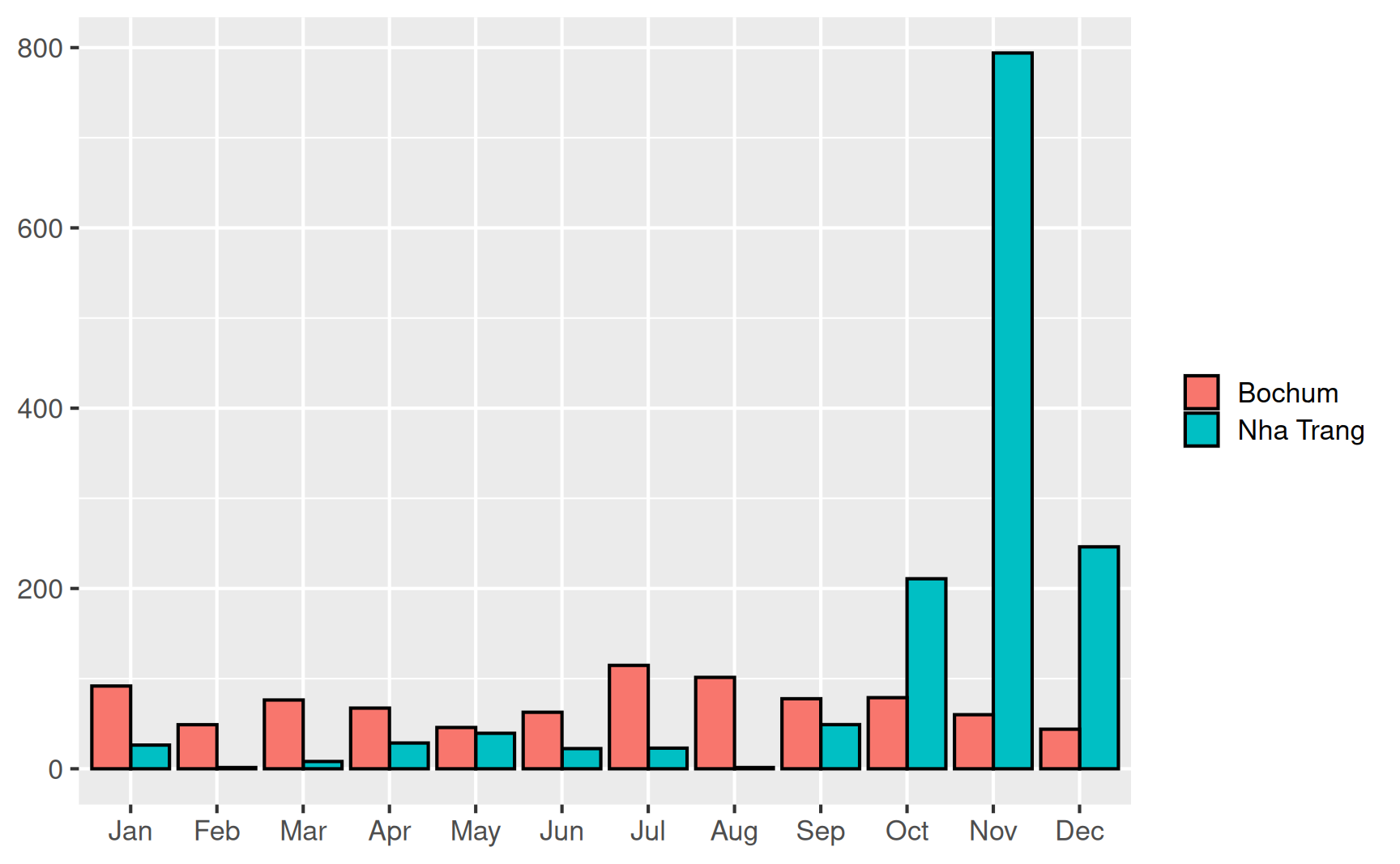
In Abbildung 7.1 sind die monatlichen Niederschläge des Jahres 2008 in Bochum und des Jahres 2015 in Nha Trang (Vietnam) zu sehen. Insgesamt sind in Bochum 869mm und in Nha Trang 1450.5mm Niederschläge gefallen. Allerdings konzentrieren sich die Niederschläge in Vietnam auf drei Monate, in allen anderen Monaten regnet es sogar weniger als in Bochum. Eine solche Konzentration von großen Beiträgen zu einer Gesamtsumme auf wenige Merkmalen wird mithilfe eines Konzentrationsmaßes quantifiziert.
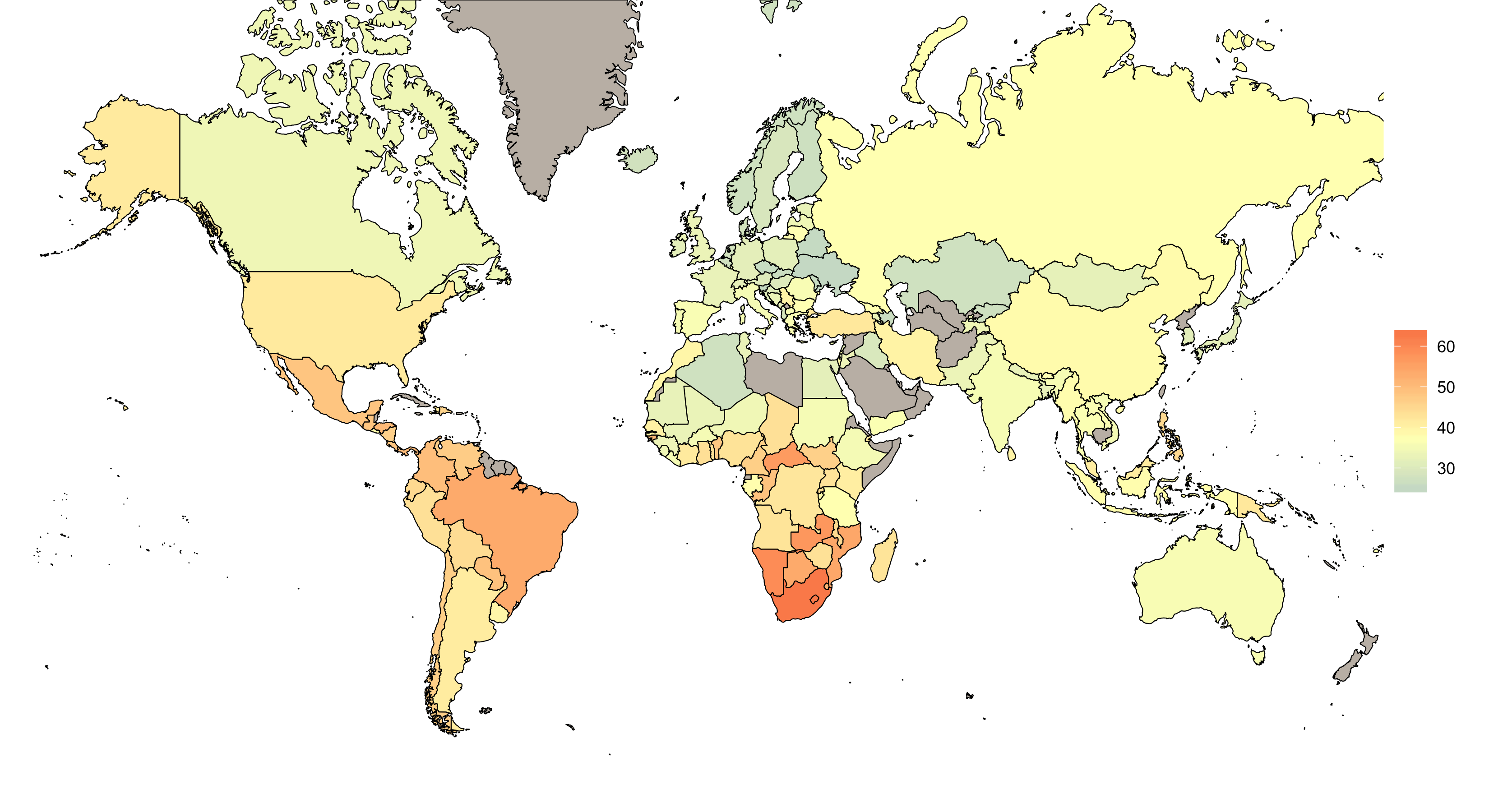
Ein wichtiges Konzentrationsmaß ist der Gini-Koeffizient, ein statistisches Maß, das vom italienischen Statistiker Corrado Gini (1884 – 1965) zur Darstellung der Ungleichverteilung von Einkommen in einer Volkswirtschaft entwickelt wurde. Zum Beispiel veröffentlicht die Weltbank Daten über die Verteilung des Wohlstandes in Ländern der Welt (siehe Abbildung 7.2). Der Gini-Koeffizient wird mithilfe der Lorenzkurve bestimmt.
7.1 Lorenzkurve
In der Lorenzkurve wird dargestellt, wie viel jeder einzelne Wert einer Stichprobe zur Summe der Werte beiträgt. Dabei werden die Beiträge ihrer Größe nach geordnet und in dieser Reihenfolge in einem \(uv\)-Koordinatensystem aufgetragen. Die Lorenzkurve verbindet diese Punkte zu einem Polygonzug. Um zu einer Darstellung zu gelangen, die nicht von der Anzahl der Beobachtungen und der Größe der Werte abhängt, werden die Daten in den Bereich von 0 bis 1 skaliert. Das Prinzip ist am folgenden Datensatz mit den drei Merkmalen A, B und C gut zu erkennen.
| A | B | C |
|---|---|---|
| 4 | 1 | 2 |
| 4 | 1 | 3 |
| 4 | 1 | 4 |
| 4 | 1 | 5 |
| 4 | 16 | 6 |
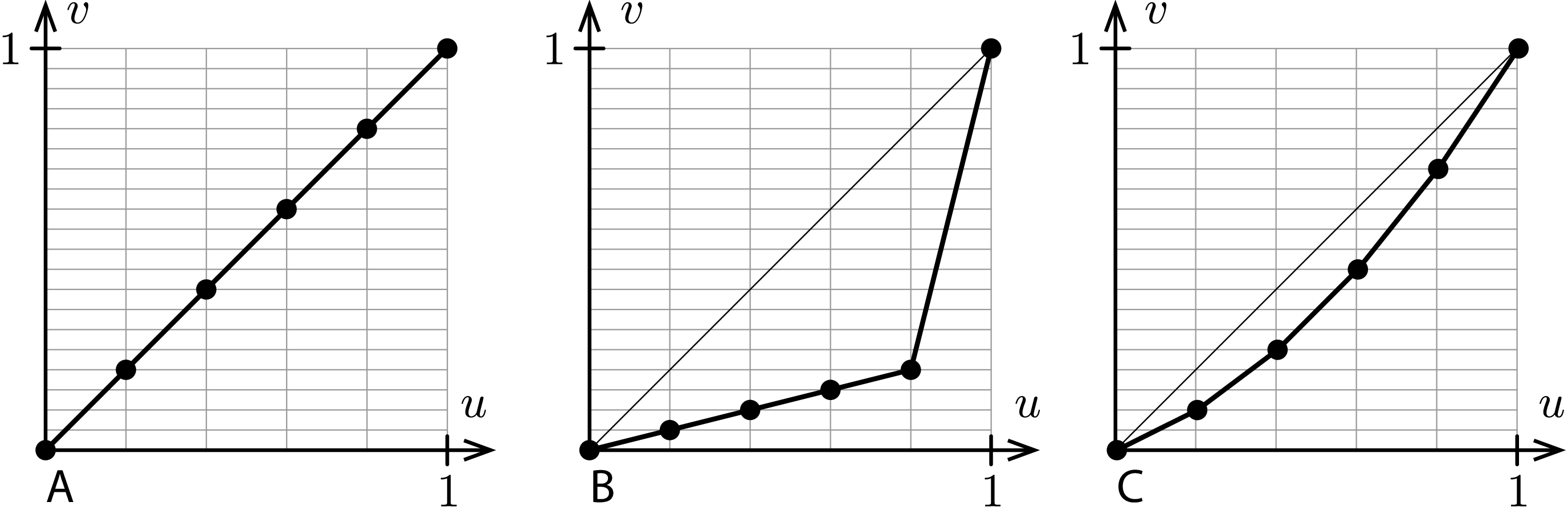
Man kann sich überlegen, dass die Lorenzkurve monoton steigend ist, wobei die Steigung der Liniensegmente nach rechts hin zunimmt oder gleich bleibt. Sind alle Werte des Merkmals gleich groß, dann ist die Lorenzkurve die Winkelhalbierende zwischen den Koordinatenachsen. Je stärker sich die Werte unterscheiden, umso größer wird der “Bauch” der Kurve.
Aus dem Beispiel oben können wir die Rechenvorschrift für die Punkte der Lorenzkurve ableiten und in der folgenden Definition festhalten.
Definition (Lorenzkurve): Für die geordnete Urliste \(x_{(1)}, x_{(2)}, \dots, x_{(n)}\) ist die Lorenzkurve der Polygonzug durch die Punkte
\[ (0, 0), (u_1, v_1), (u_2, v_2), \dots, (u_n, v_n) \]
mit den Koordinaten
\[ u_j = \frac{1}{n} \cdot j \quad \text{und} \quad v_j = \frac{1}{s} \cdot \sum_{i=1}^j x_i \quad \text{wobei} \quad s = \sum_{i=1}^n x_i. \]
Damit ist auch klar, dass \(u_n = v_n = 1\) gelten muss.
Für die Niederschläge in Bochum und Nha Trang erhalten wir mit den sortierten Monatswerten
die beiden Lorenzkurven
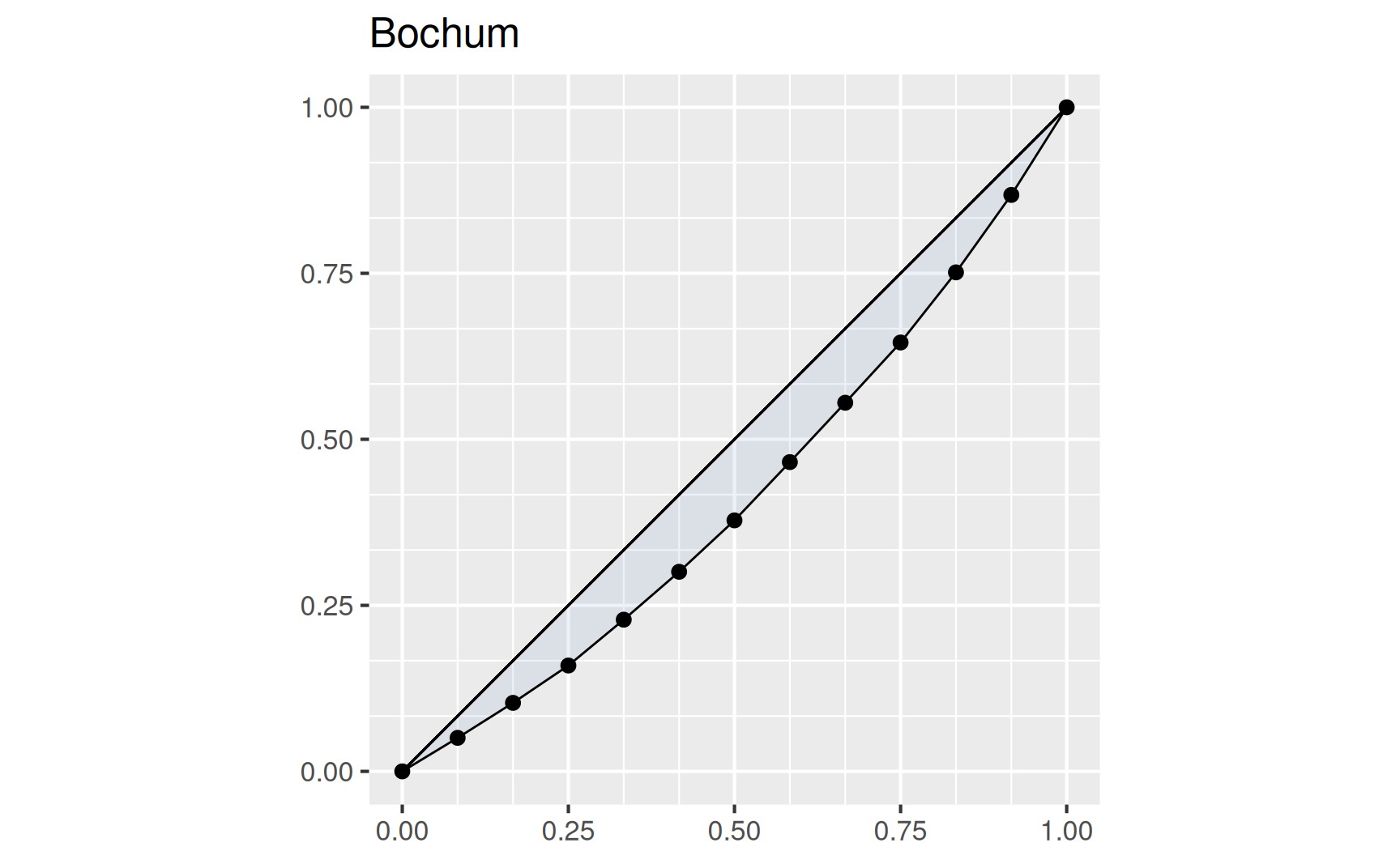
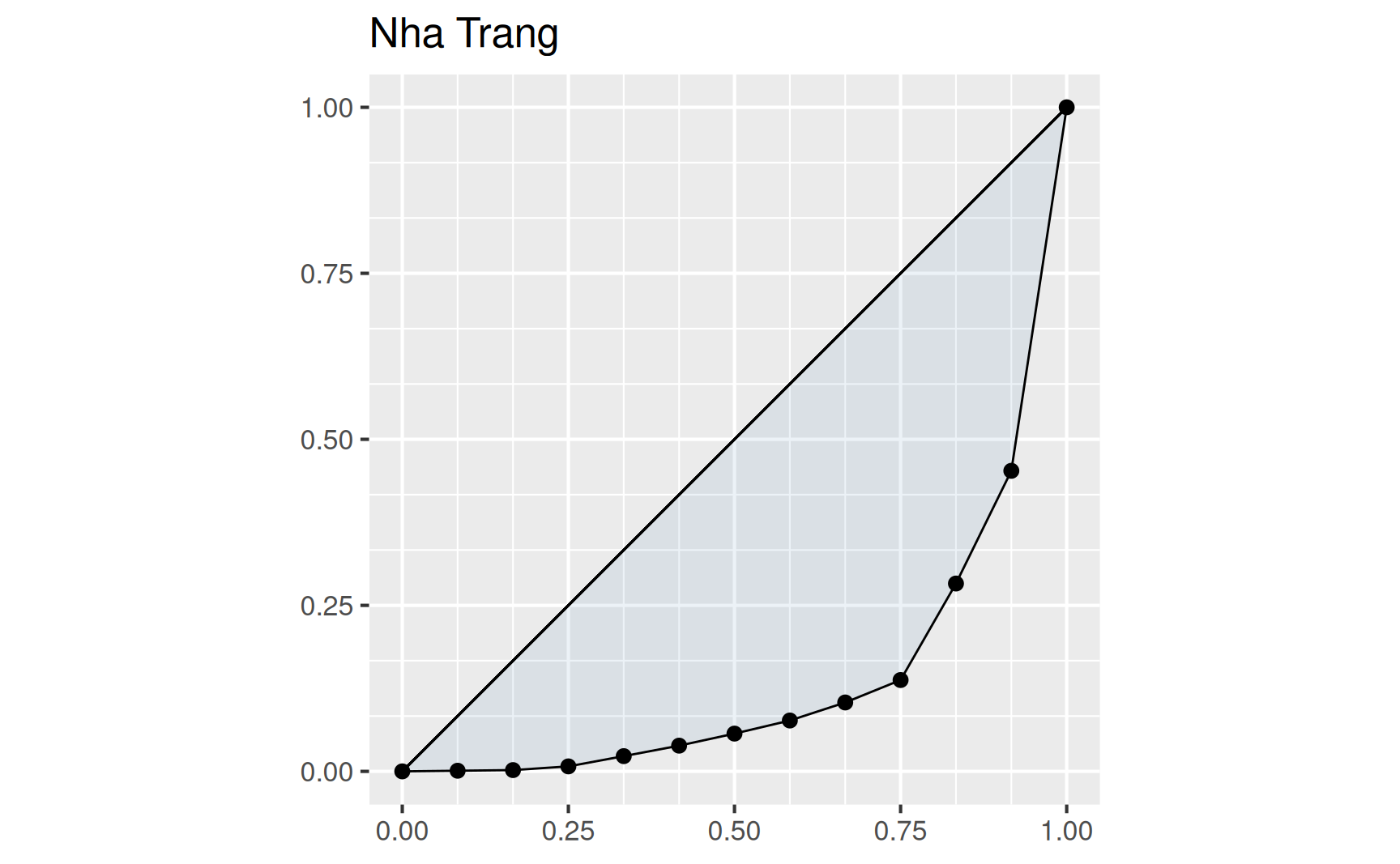
Die starke Konzentration der Jahresniederschläge in Nha Trang ist an dem Verlauf der zugehörigen Lorenzkurve abzulesen: In insgesamt 75% der Zeit des Jahres fallen gerade einmal ca. 12.5% der Jahresniederschläge.
7.2 Der Gini-Koeffizient
Die Stärke der Konzentration drückt sich in der Entfernung der Lorenzkurve von der Diagonalen aus. Es ist daher naheliegend, die Fläche zwischen der Diagonalen und der Lorenzkurve als Maß für die Konzentration des Merkmals zu verwenden. Diese Fläche wird noch auf die Fläche des Dreiecks unter der Winkelhalbierenden bezogen.
Definition (Gini-Koeffizient): Der Gini-Koeffizient ist
\[ G = \frac{\text{Fläche zwischen Diagonale und Lorenzkurve}}{\text{Fläche zwischen Diagonale und $u$-Achse}} \]
\[ = 2 \cdot \text{Fläche zwischen Diagonale und Lorenzkurve}. \]
Für den Gini-Koeffizienten gibt es zwei Extremfälle:
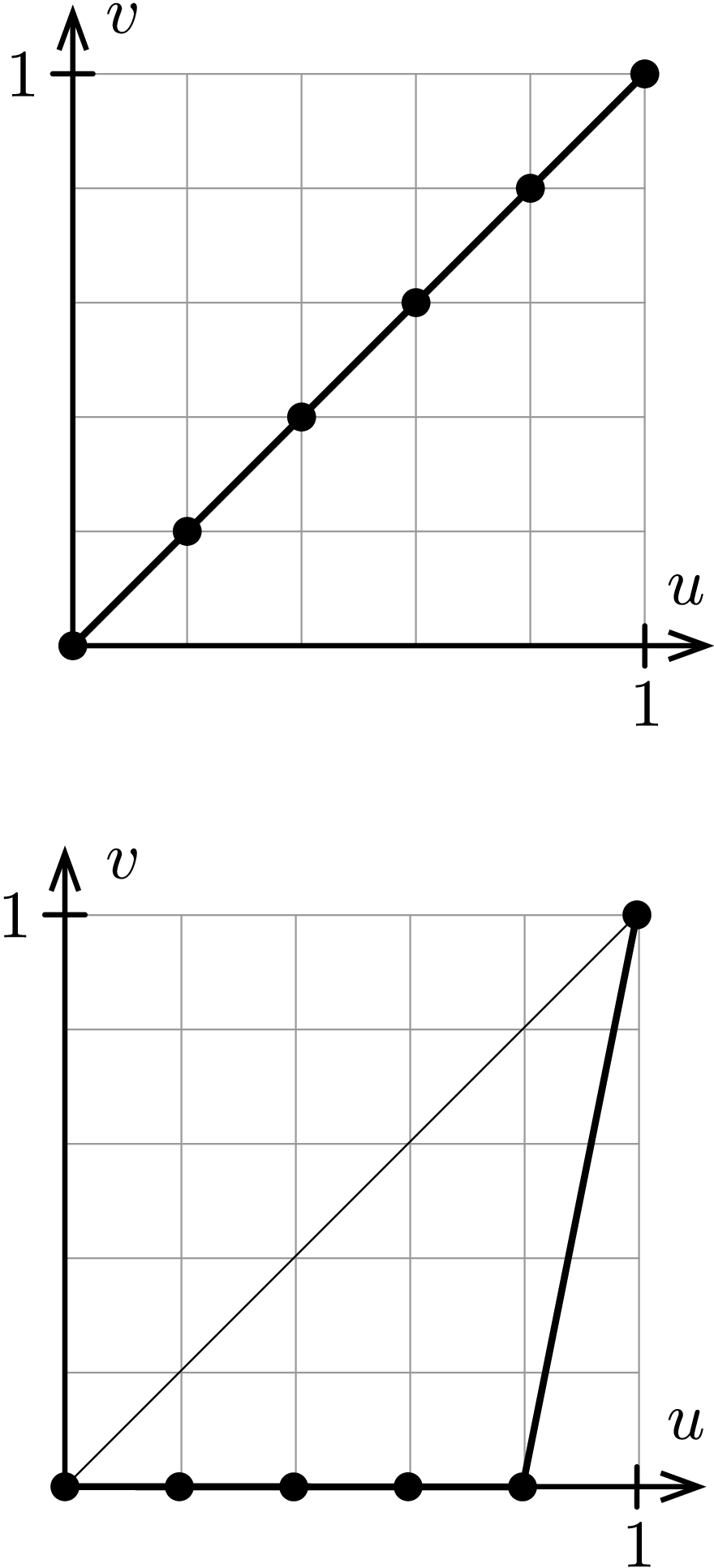
Alle Werte in der Stichprobe sind gleich. Dann ist die Lorenzkurve gleich der Diagonalen und der Gini-Koeffizient wird minimal: \[ G_{min} = 0. \]
Nur ein Wert ist ungleich Null. Hier verläuft die Lorenzkurve bis zum vorletzten Punkt auf der horizontalen Achse. Da der horizontale Abstand zwischen den Punkten \(1/n\) beträgt, ergibt sich der maximale Gini-Koeffizient \[ G_{max} = 2 \cdot (1/2 - 1/2 \cdot 1 \cdot 1/n) = (n-1)/n. \]
Wir sehen, dass der maximale Gini-Koeffizient von der Anzahl der Beobachtungen abhängt. Dieser unerwünschte Effekt wird mit dem normierten Gini-Koeffizienten umgangen.
Definition (Lorenz-Müller-Koeffizient): Der Gini-Koeffizient wird mit dem Faktor \(n/(n-1)\) multipliziert und wir erhalten den normierten Gini-Koeffizienten
\[ G^* = \frac{n}{n-1}G \]
mit dem Wertebereich \(G^* \in [0, 1]\), der manchmal auch als Lorenz-Münzer-Koeffizient bezeichnet wird.
Für die Jahresniederschläge aus dem einleitenden Beispiel erhalten wir die Zahlenwerte der normierten Gini-Koeffizienten für
\[ \begin{aligned} \text{Bochum:} \quad G^* = 0.18, \\ \text{Nha Trang:} \quad G^* = 0.79. \end{aligned} \]
Hier ist an einer Zahl unmittelbar zu erkennen, dass die Niederschläge in Bochum sehr viel gleichmäßiger über das Jahr verteilt gefallen sind als in Nha Trang.
Informationsverlust. Wie bei allen Maßzahlen für Verteilungen stellt auch der Gini-Koeffizient eine Vereinfachung dar. Insbesondere können zwei völlig unterschiedliche Verteilungen zum selben Gini-Koeffizienten führen. Mit der Reduktion ist also ein Verlust an Informationen verbunden.
Wir betrachten hierzu als Beispiel zwei Gruppen von je zehn Personen, die jeweils den angegebenen Betrag im Geldbeutel haben.
| Gruppe | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | \(\sum\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 9 | 9 | 9 | 9 | 9 | 81 | 81 | 81 | 81 | 81 | 450 |
| B | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 225 | 450 |
Es liegt folgende Situation vor:
In Gruppe A haben die ärmeren fünf Personen insgesamt \(5 \cdot 9 / 450 \cdot\) 100% = 10% des gesamten Geldes in der Tasche. Die anderen fünf Personen teilen sich die verbleibenden 90%.
In Gruppe B haben neun Personen die eine Hälfte des Geldes, eine weitere Person besitzt die andere Hälfte.
Mit diesen Überlegungen ist klar, dass die Lorenzkurven der beiden Verteilungen folgendermaßen aussehen müssen:
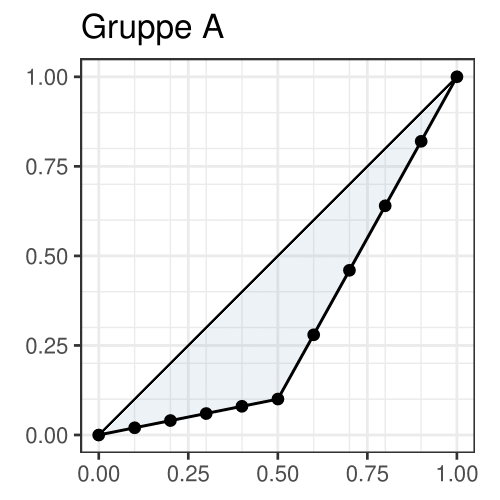
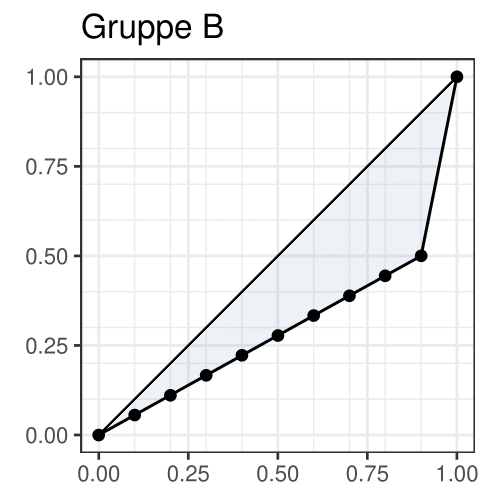
Die zugehörigen normierten Gini-Koeffizienten bestimmen wir elementar-geometrisch
\[ \text{Gruppe A:} \quad G^* = \frac{10}{9} \cdot 2 \cdot \left( \frac{1}{2} - \left( \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{10} + \frac{1}{2} \cdot \frac{1}{2} \cdot \left(\frac{1}{10} + 1 \right) \right) \right) = \frac{4}{9} \]
\[ \text{Gruppe B:} \quad G^* = \frac{10}{9} \cdot 2 \cdot \left( \frac{1}{2} - \left( \frac{1}{2} \cdot \frac{9}{10} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{10} \cdot \left(\frac{1}{2} + 1 \right) \right) \right) = \frac{4}{9} \]
und stellen fest, dass sich jeweils derselbe Wert ergibt. Wenn man sich die beiden Lorenz-Kurven genauer anschaut ist dieses Ergebnis nicht überraschend: Die jeweils andere Kurve ergibt sich aus einer Spiegelung an der Geraden \(1-x\). Somit ist die eingeschlossene Fläche natürlich gleich.