3  Untersuchung einzelner Merkmale

In diesem Abschnitt geht es darum, wie sich für eine Erhebung die Verteilung einzelner Merkmale bestimmen und darstellen lassen. Man kann dabei zunächst einfach zählen, wie oft bestimmte Werte vorkommen und erhält daraus Häufigkeiten und Häufigkeitsverteilungen. Gibt es eine große Zahl verschiedener Ausprägungen, dann ist es übersichtlicher, die Werte in Klassen einzuteilen und ein Histogramm zu erzeugen. Darüber hinaus können Verteilungen (als Häufigkeitsverteilung oder Histogramm) hinsichtlich ihrer Modalität und Schiefe klassifiziert werden. Schließlich erhalten wir mit der empirischen Verteilungsfunktion noch eine alternative Sicht auf die Verteilung der Werte.

Die Beschränkung auf ein einzelnes Merkmal bedeutet, dass wir uns nun aus einem Datensatz vom Umfang \(n\) ein einzelnes Merkmal \(X\) mit den Werten \(x_1, x_2, \dots, x_n\) herausgreifen. Es ist klar, dass es sehr schwer ist, aus diesen Rohdaten unmittelbar etwas abzulesen, sobald es sich um mehr als eine Handvoll Werte handelt.

3.1 Häufigkeitsverteilung

In vielen Fällen ergibt sich ein guter Eindruck über ein Merkmal, wenn gezählt wird, wie oft einzelne Ausprägungen in den Werten zu finden sind. Das Ergebnis dieser Zählung ist die Häufigkeitsverteilung.

Um die Häufigkeitsverteilung zu bestimmen, muss zunächst geschaut werden, welche Ausprägungen in den Rohdaten überhaupt vorkommen. Wir bezeichnen die Elemente dieser Menge mit \(a_1, a_2, \dots, a_k\) und halten fest, dass \(k \leq n\) gelten muss. In der Regel werden die Werte nach einem geeigneten Kriterium sortiert (Zahlenwert, Anfangsbuchstabe, Wochentag etc.).

Als absolute Häufigkeit der Ausprägung \(a_j\) bezeichnen wir nun die Anzahl der Werte aus der Urliste \(x_1, x_2, \dots, x_n\), die mit \(a_j\) übereinstimmen. Wird die absolute Häufigkeit durch den Stichprobenumfang \(n\) geteilt, dann ergibt sich die relative Häufigkeit.

Definition (absolute und relative Häufigkeit): Für die Werte eines Merkmals \(x_1, x_2, \dots, x_n\) mit den unterschiedlichen Ausprägungen \(a_1, a_2, \dots, a_k\) verwenden wir folgende Bezeichnungen.

\(h(a_j)\):

absolute Häufigkeit der Ausprägung \(a_j\). Der Wert \(h(a_j)\) gibt an, wie oft die Ausprägung \(a_j\) in den Werten \(x_1, x_2, \dots, x_n\) vorkommt,

\(f(a_j) = h(a_j)/n\):

relative Häufigkeit der Ausprägung \(a_j\).

Mit den Abkürzungen \(h_j = h(a_j)\) und \(f_j = f(a_j)\) heißen die Zahlenfolgen

\(h_1, h_2, \dots, h_k\):

absolute Häufigkeitsverteilung,

\(f_1, f_2, \dots, f_k\):

relative Häufigkeitsverteilung.

3.1.1 Grafische Darstellung von Häufigkeitsverteilungen

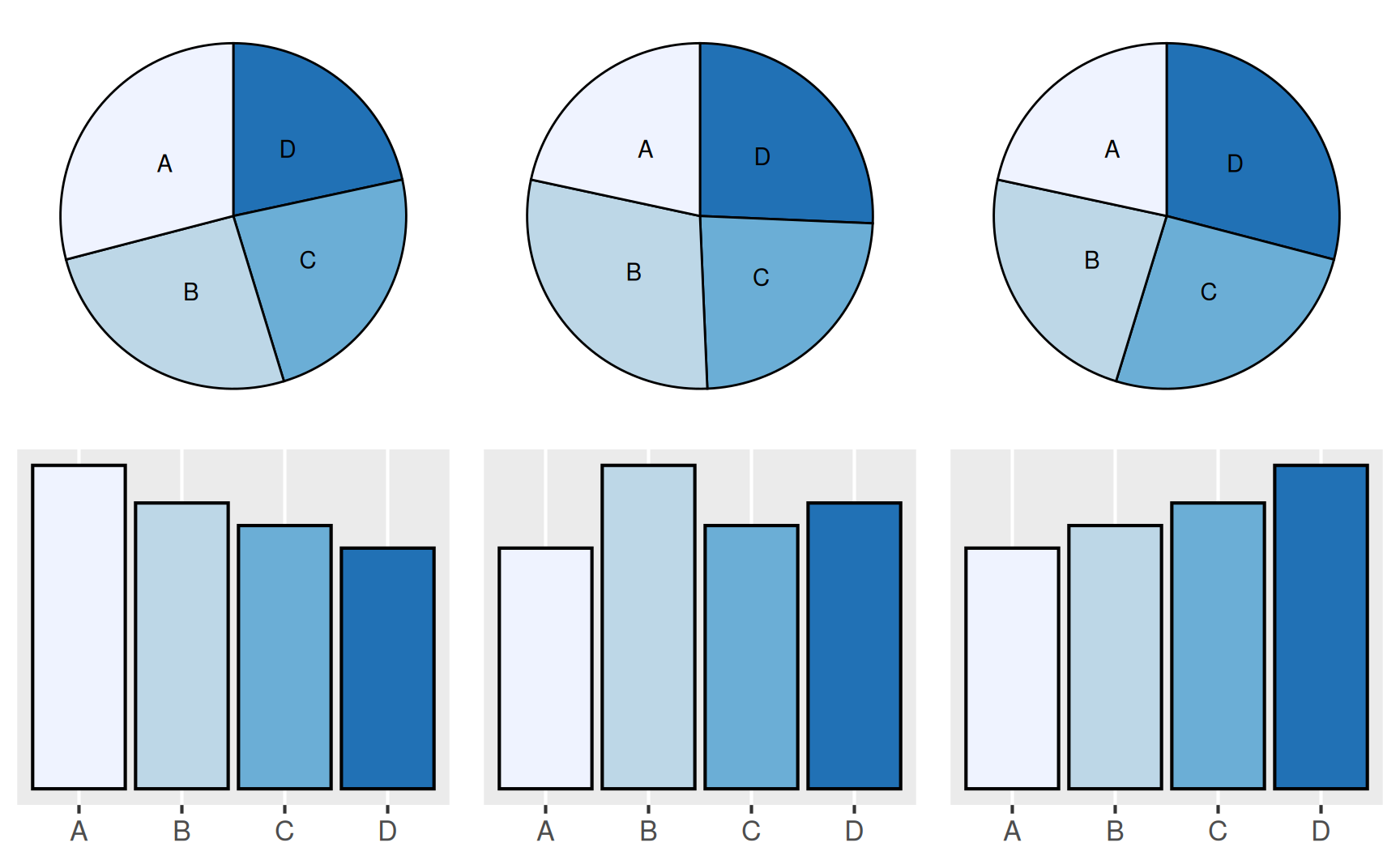
Die Häufigkeitsverteilungen lassen sich natürlich tabellarisch aufbereiten, häufig ist aber eine grafische Darstellung besser geeignet. Die gebräuchlichsten Darstellungsformen sind Stab-, Säulen-, Balken- und Kreisdiagramme. Als Alternative zu Kreisdiagrammen werden häufig auch Ringdiagramme verwendet. In Abbildung 3.1 sind diese Diagrammtypen beispielhaft dargestellt.

Diagrammtypen

Stabdiagramm:

Zahlenwerte für \(h_1, h_2, \dots, h_n\) (oder \(f_1, f_2, \dots, f_n\)) werden mit einem senkrechten Strich angetragen.

Säulendiagramm:

Wie das Stabdiagramm aber mit Rechtecken anstatt Strichen.

Balkendiagramm:

Das Säulendiagramm um 90° gedreht.

Kreisdiagramm:

Der vom \(j\)-ten Kreissektor eingeschlossene Winkel beträgt \(\alpha_j = f_j \cdot 360°\). Die Flächen der Kreissektoren sind damit proportional zu den Häufigkeiten.

 

 

 

 

Abbildung 3.1: Gebräuchliche Diagrammtypen (Stab-, Säulen-, Balken-, Kreis- und Ringdiagramm) zur Darstellung von Verteilungen (Energieträger Bundesrepublik Deutschland 2017, Datenquelle: BMWI)

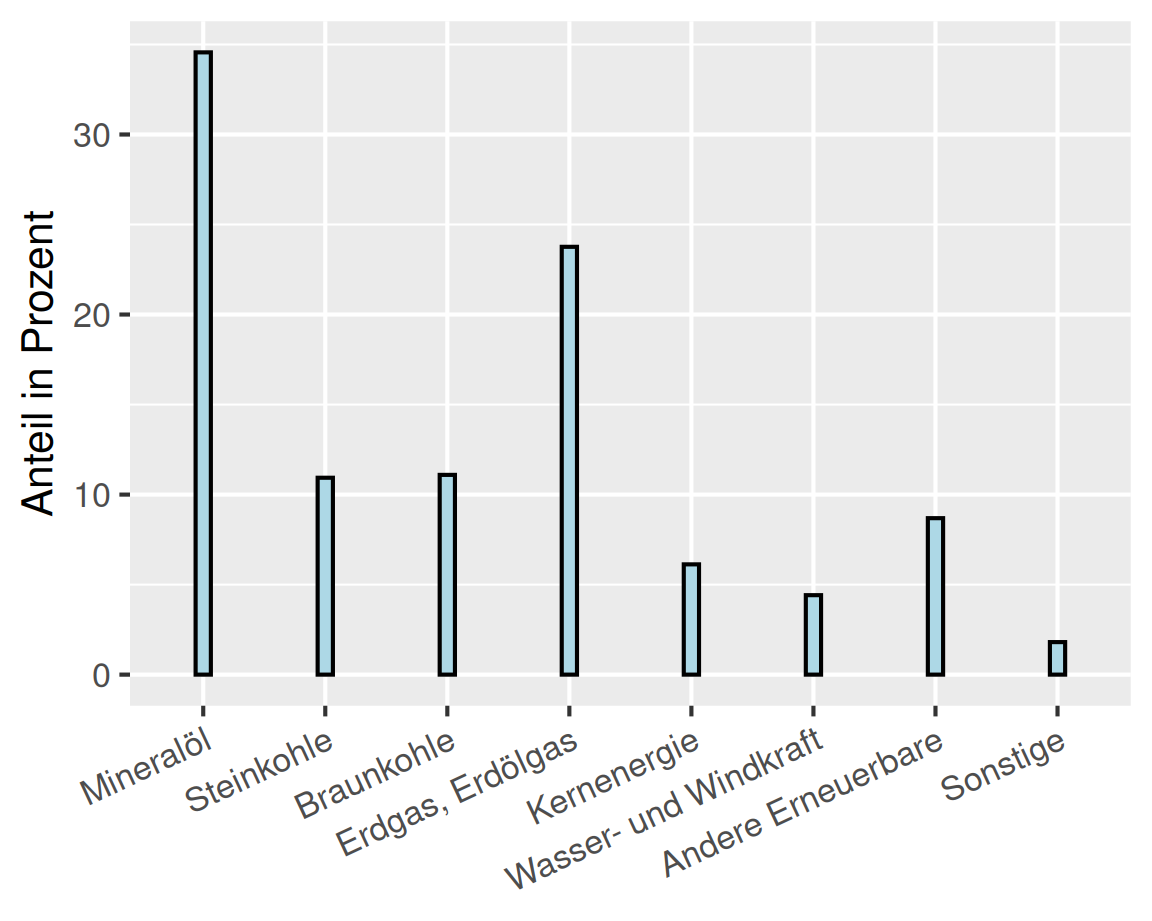
Kritik an Kreisdiagrammen. Obwohl Kreisdiagramme in der Praxis sehr häufig verwendet werden sind sie nicht ganz unproblematisch. Das hat mehrere Gründe:

• Längen sind leichter zu unterscheiden als Winkel (siehe Abbildung 3.2).

• Die Diagramme werden für viele Merkmalsausprägungen schnell unübersichtlich.

• Wenn Verteilungen verglichen werden sollen, dann müssen zwei Kreisdiagramme erstellt werden.

• Die Darstellung der zeitlichen Entwicklung einer Verteilung ist nicht möglich (siehe Abbildung 3.3).

Abbildung 3.2: Drei Verteilungen jeweils in einem Kreis- und einem Säulendiagramm dargestellt. Die Kreisdiagramme unterscheiden sich auf den ersten Blick nur unwesentlich voneinander und die Eigenschaften der Verteilungen werden nicht klar ersichtlich

Abbildung 3.3: Zeitliche Entwicklung einer Verteilung in einem Säulendiagramm (Energieträger Bundesrepublik Deutschland 1990 - 2017, Quelle: BMWI)

3.2 Histogramme

Wenn ein Merkmal viele verschiedene Ausprägungen besitzt, das heißt, wenn die meisten Ausprägungen nur ein oder zwei mal vorkommen, dann ist die Darstellung einer Verteilung nicht informativ. Das ist zum Beispiel fast immer dann der Fall, wenn es sich um stetige oder quasi-stetige Merkmale handelt.

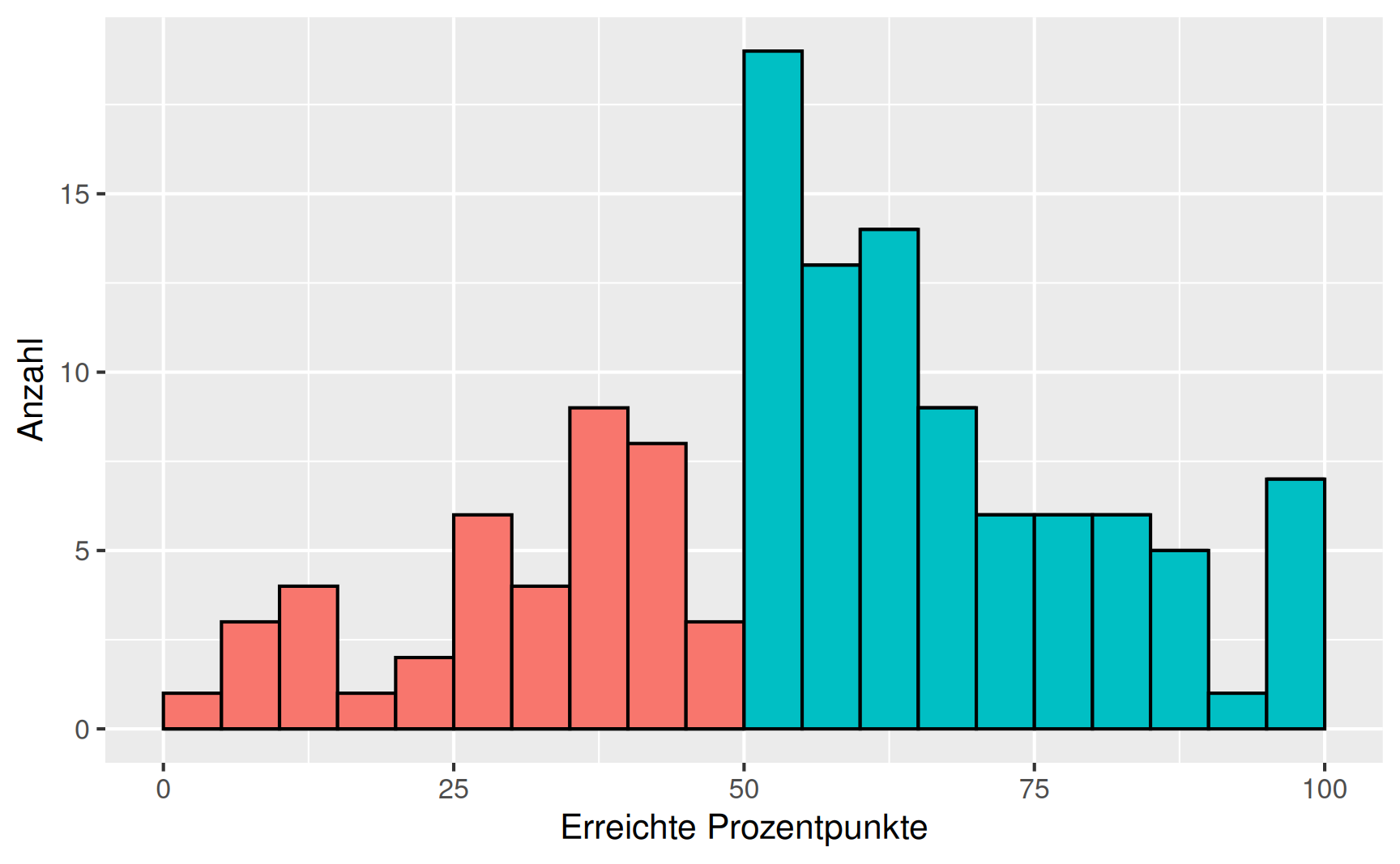
Beispiel Klausurergebnisse: Wir betrachten die Ergebnisse einer Klausur im Fach Mathematik mit knapp 130 Teilnehmern. Die erreichten Prozentpunkte bilden die Urliste

\[ x_1 = 28.17, x_2 = 12.32, x_3 = 59.58, x_4 = 55.02, \dots, x_{129} = 87.34. \]

Die zugehörige Häufigkeitsverteilung ist nachfolgend dargestellt.

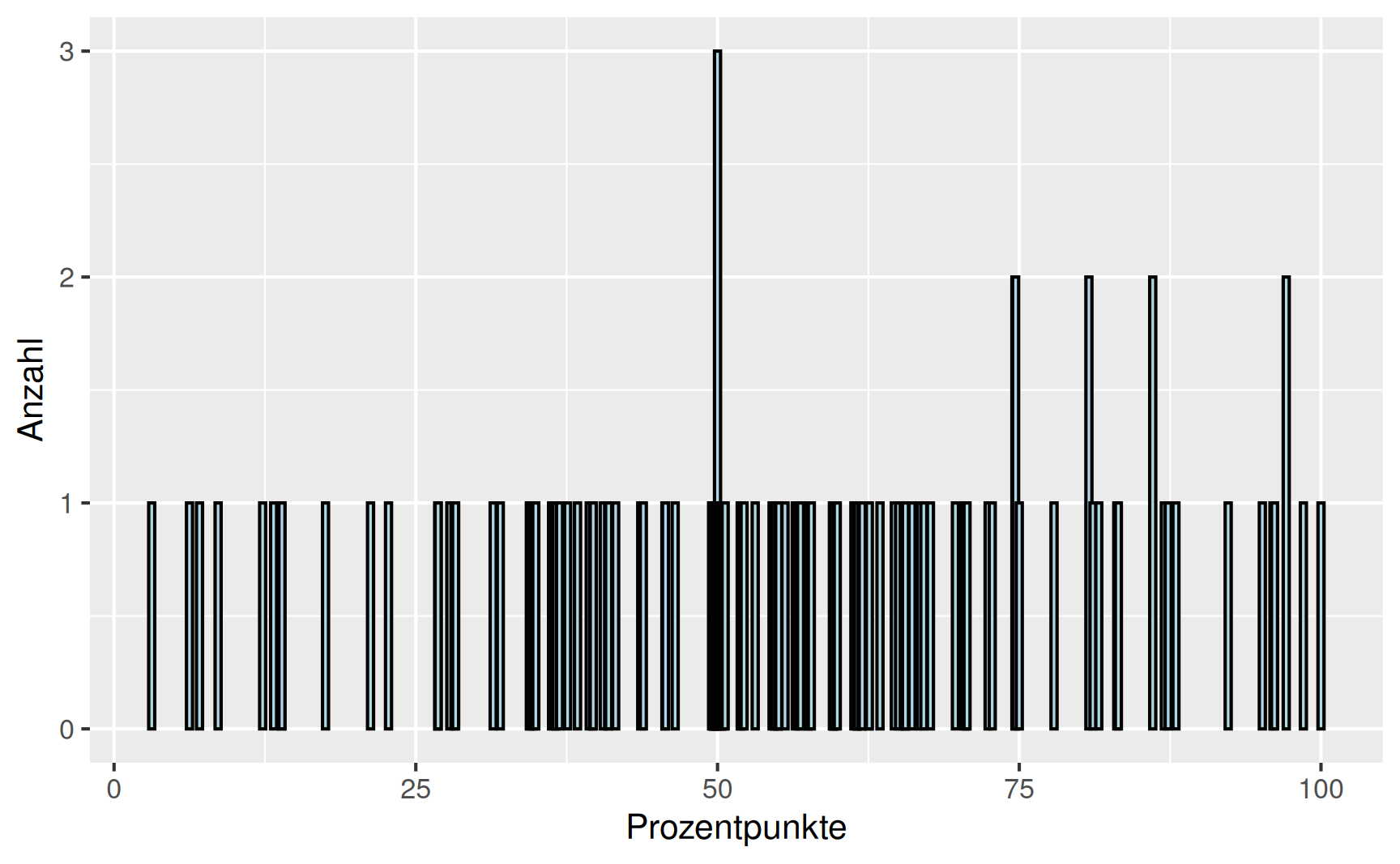
Es ist zu erkennen, dass einzelne Werte zwei- oder dreimal vorkommen und dass es eine Häufung um 50% herum gibt. Darüber hinaus ist das Diagramm nicht sonderlich informativ.

Um Merkmale mit einer großen Zahl an verschiedenen Ausprägungen übersichtlich darzustellen, werden die Daten zunächst in Gruppen zusammengefasst. Für die Gruppen wird dann eine Häufigkeitsverteilung ermittelt und in einem so genannten Histogramm grafisch dargestellt.

Ein Histogramm entsteht in drei Schritten. Wir gehen dabei davon aus, dass es sich um ein zahlenwertiges Merkmal handelt.

1. Für die Gruppierung der Daten wählen wir als Klassen die \(k\) benachbarten Intervalle \[[c_0, c_1), [c_1, c_2), \dots, [c_{k-1}, c_k) \quad \text{mit} \quad c_j < c_{j+1}\]. Die Intervalle sind auf einer Seite geschlossen und auf der anderen Seite offen, so dass jeder Wert \(x_j\) in genau einer Klasse enthalten ist. Wichtig ist, dass \(c_0\) kleiner gleich der kleinsten Ausprägung und \(c_k\) größer als die größte Ausprägung des betrachteten Merkmals ist.

Anmerkung: Die Intervalle hätten wir genauso gut in der Form \((c_j, c_{j+1}]\) (also linksoffen) wählen können, das macht keinen grundlegenden Unterschied.

1. Wir zählen für jede Klasse wie viele Ausprägungen sie enthält und erhalten die absolute Häufigkeitsverteilung \(h_1, h_2, \dots, h_k\). Die Werte können natürlich auch noch auf den Umfang der Stichprobe bezogen werden, dann ist \(f_j = h_j / n\) die relative Häufigkeitsverteilung der Klassen.

2. Die Zahlenwerte werden in einem Säulendiagramm dargestellt. Am einfachsten wäre es jetzt, die Höhe der Säulen proportional zu \(h_j\) beziehungsweise \(f_j\) anzutragen. Allerdings würde das zu einer verzerrten Wahrnehmung der Daten führen, falls die Klassen nicht alle gleich breit sind. Das liegt daran, dass unser Auge für ein Rechteck primär die Fläche und nicht die Höhe wahrnimmt. Wir wählen daher die Höhe des Rechtecks so, dass die Fläche der Säule proportional zur jeweiligen Häufigkeit ist. Aus der Beziehung “Fläche = Breite \(\times\) Höhe’’ und mit der Klassenbreite \(d_j = c_j - c_{j-1}\) entspricht die Höhe dann dem Wert \(h_j / d_j\) oder \(f_j / d_j\). Damit ist das Histogramm nach dem Prinzip der Flächentreue konstruiert.

Für die Wahl der Klassen gibt es keine festen Vorgaben, letztlich geht es einfach darum, dass die Eigenschaften der Daten anhand des Diagramms möglichst gut zu erkennen sind. In der Regel wird man versuchen, die Klassenbreiten \(d_j\) gleich groß zu wählen. Für die Anzahl der Klassen gibt es die Faustregeln

\[ k \approx \sqrt{n} \quad \text{oder} \quad k \approx 10 \log_{10} n, \]

aber letztlich entscheidet der subjektive Eindruck.

Beispiel Klausurergebnisse (Fortsetzung): Mit den Klassen \[[0, 5), [5, 10), \dots, [95, 101)\]

ergibt sich für die Mathematikklausur folgendes Histogramm:

3.3 Grobe Charakterisierung von Häufigkeitsverteilung

Für die Charakterisierung der Häufigkeitsverteilung von Merkmalen gibt es zwei wichtige Kriterien. Man spricht von unimodalen oder multimodalen Verteilungen und von symmetrischen oder schiefen Verteilungen. Die Begriffe sind sowohl für Häufigkeitsverteilungen als auch für Histogramme üblich.

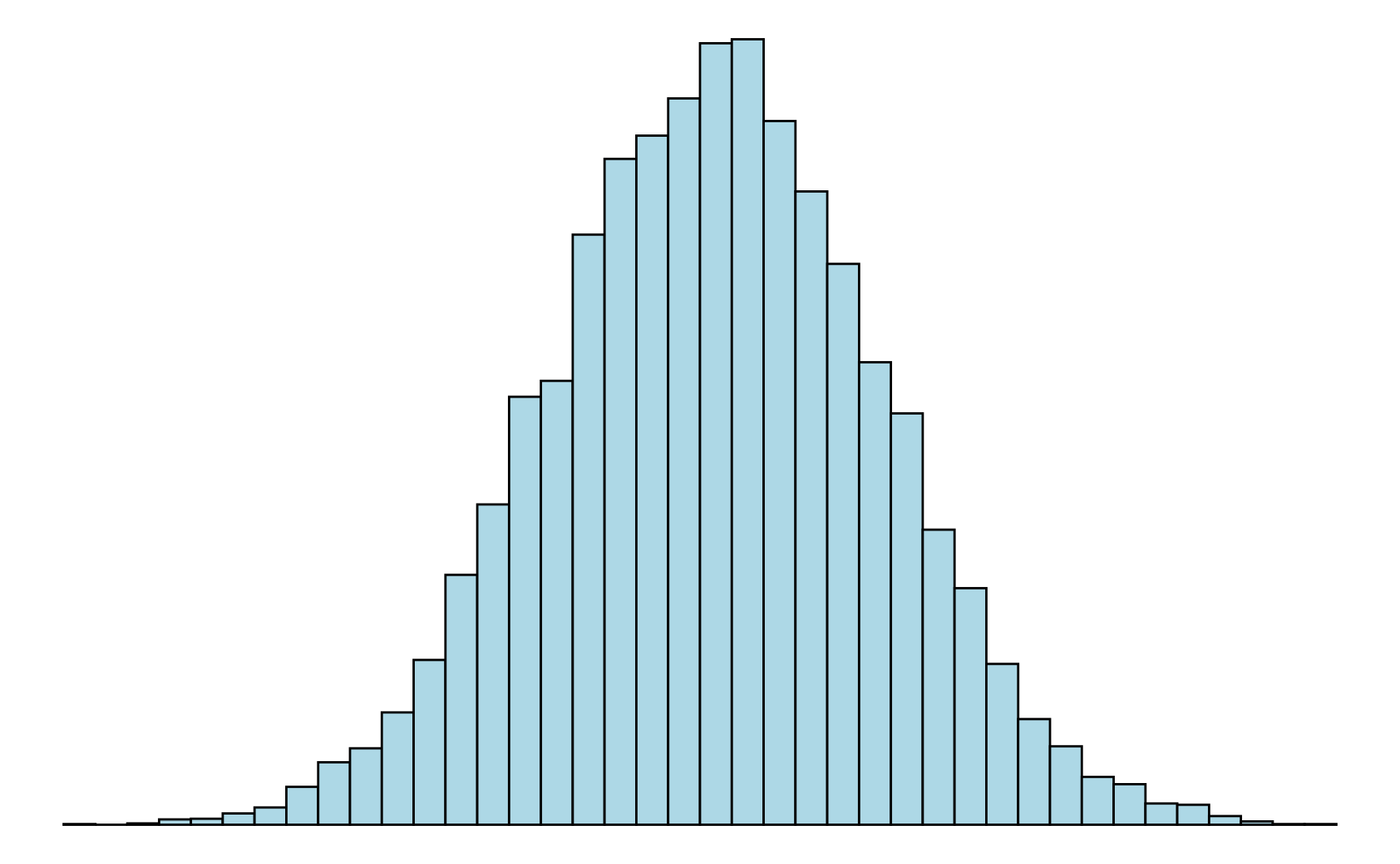
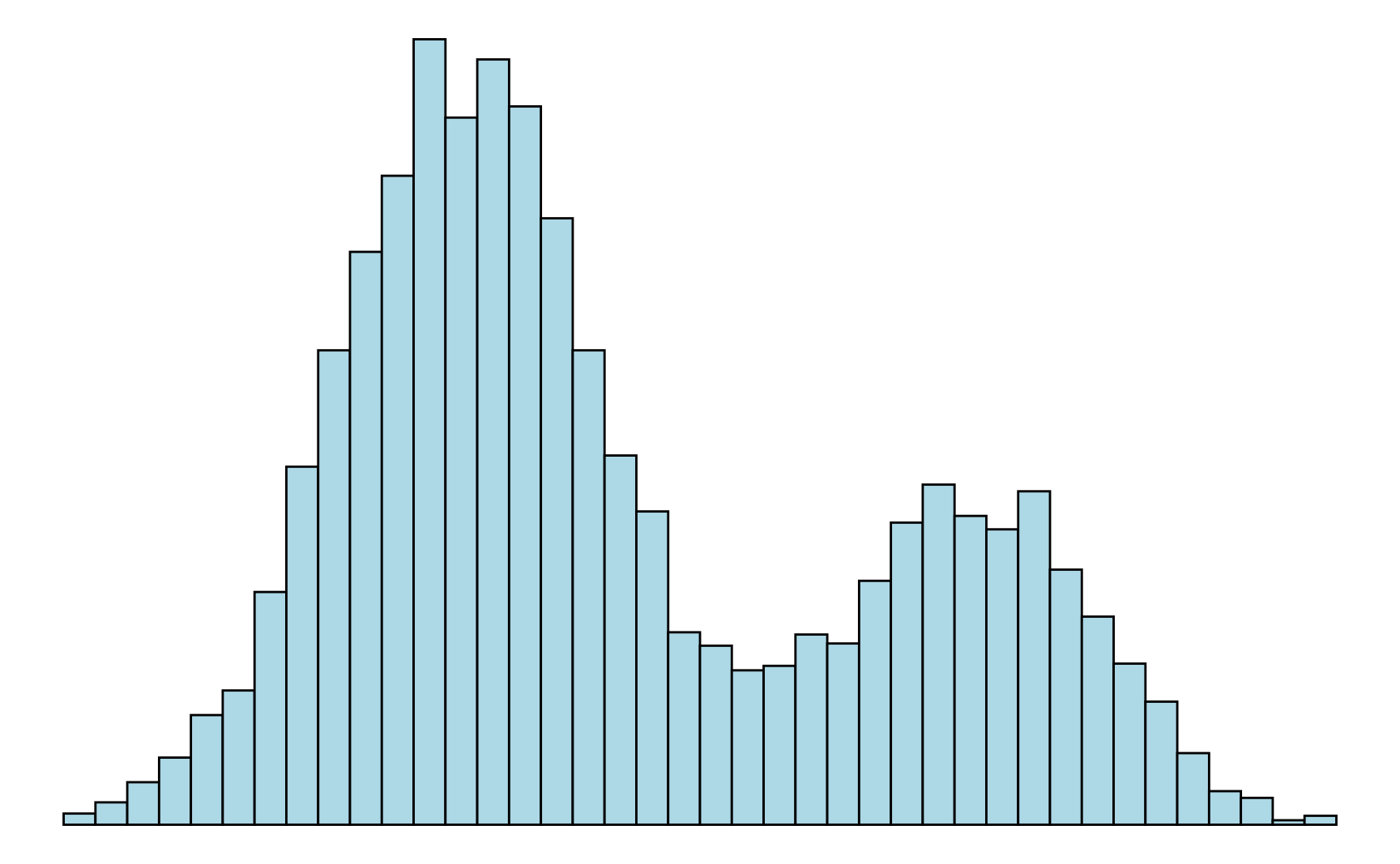
Unimodale und multimodale Verteilungen. Eine Verteilung, die einen Gipfel aufweist, von dem die Häufigkeiten zu den Randbereichen hin abfallen, ohne dass ein weiterer deutlich ausgeprägter Gipfel hervortritt, heißt unimodal (Eingipfelig). Treten weitere Gipfel deutlich hervor, so spricht man von einer multimodalen Verteilung. Sind es genau zwei Gipfel, dann nennt man die Verteilung bimodal (siehe Abbildung 3.4).

(a) Unimodal

(b) Bimodal

(c) Multimodal

Abbildung 3.4: Modalität von Verteilungen

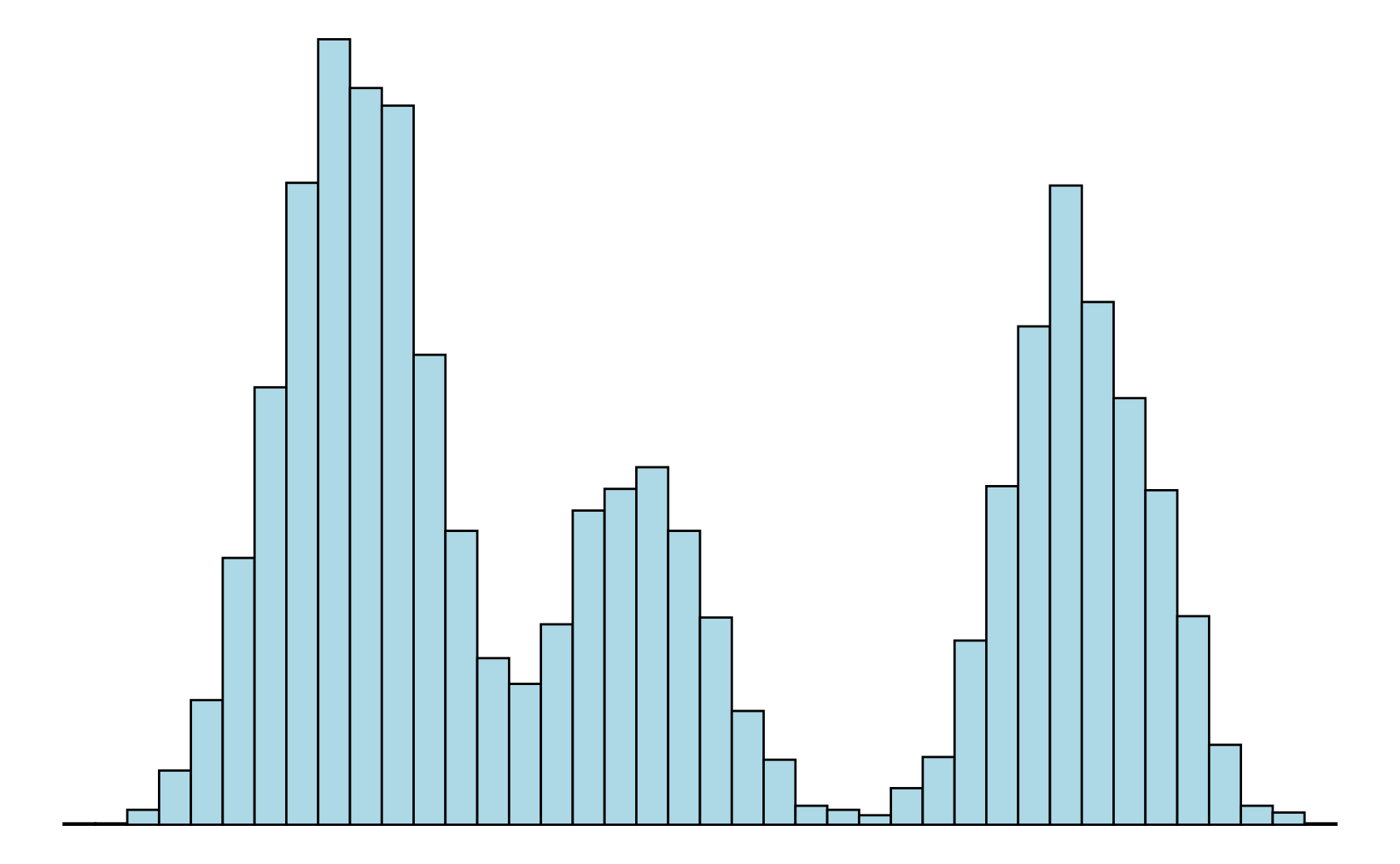
Symmetrische und schiefe Verteilungen. Gibt es für eine Verteilung eine Symmetrieachse, so dass der Verlauf links und rechts von dieser Achse annähernd gleich ist, dann handelt es sich um eine symmetrische Verteilung. Wichtig ist dabei, dass die Verteilung nicht exakt symmetrisch verlaufen muss, um als symmetrisch zu gelten. Ist die Verteilung deutlich unsymmetrisch, dann handelt es sich um eine schiefe Verteilung. Eine unimodale Verteilung, die nach links hin sehr steil abfällt, wird linkssteil(oder rechtsschief) genannt. Entsprechend heißt eine Verteilung, die nach rechts hin steil abfällt rechtssteil(oder linksschief) (vergleiche Abbildung 3.5).

(a) Linkssteil bzw. rechtsschief

(b) Symmetrisch

(c) Rechtssteil bzw. linksschief

Abbildung 3.5: Schiefe von Verteilungen

3.4 Kumulierte Häufigkeitsverteilung und empirische Verteilungsfunktion

An der empirischen Verteilungsfunktion eines Merkmals lässt sich zu einem gegebenen Wert ermitteln, welcher Anteil der Ausprägungen kleiner oder gleich diesem Wert ist. Grundlage für diese Funktion bildet die absolute kumulierte Häufigkeitsverteilung.

Absolute kumulierte Häufigkeitsverteilung. Häufig stellt sich für ein bestimmtes Merkmal einer Erhebung die Frage, wie viele der Werte \(x_1, x_2, \dots, x_n\) kleiner oder gleich einem bestimmten Grenzwert \(x\) sind. So kann man zum Beispiel bei einer Klausur fragen, wie viele Studierende durchgefallen sind, das heißt in der Prüfung \(49\) oder weniger Prozentpunkte erreicht haben. Selbstverständlich könnte man die entsprechenden Werte einfach zählen, einen bildhaften Eindruck liefert jedoch eine Darstellung der absoluten kumulierten Häufig-keits-ver-teilung des Merkmals. Es handelt sich dabei um eine Funktion, die üblicherweise mit \(H\) bezeichnet wird. Am einfachsten ist das an einem Beispiel zu sehen.

Beispiel Häufigkeitsverteilung: Wir betrachten ein Merkmal mit den Werten

\[ x_1 = 1.1, x_2 = 1.3, x_3 = 1.9, x_4 = 2.5, x_5 = 2.1, x_6 = 1.3, x_7 = 4 \]

und der dargestellten Häufigkeitsverteilung.

Ausprägung	Häufigkeit
1.1	1
1.3	2
1.9	1
2.1	1
2.5	1
4.0	1

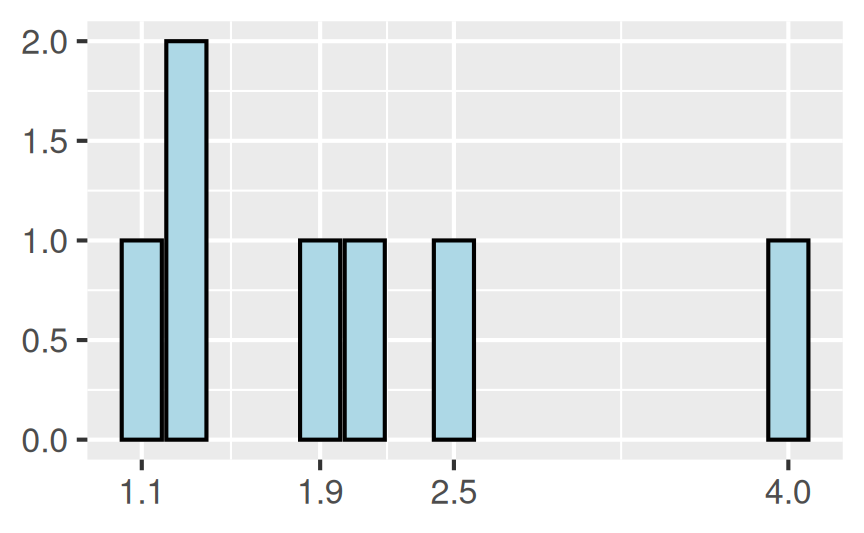
Die absolute kumulierte Häufigkeitsverteilung \(H\) sagt uns nun zu jeder Zahl \(x\), wie viele Ausprägungen kleiner oder gleich diesem Wert sind.

\[ H(x) = \begin{cases} \; 0 & \text{für} \quad x < 1.1 \\ \; 1 & \text{für} \quad 1.1 \leq x < 1.3 \\ \; 3 & \text{für} \quad 1.3 \leq x < 1.9 \\ \; 4 & \text{für} \quad 1.9 \leq x < 2.1 \\ \; 5 & \text{für} \quad 2.1 \leq x < 2.5 \\ \; 6 & \text{für} \quad 2.5 \leq x < 4 \\ \; 7 & \text{für} \quad x \geq 4 \end{cases} \]

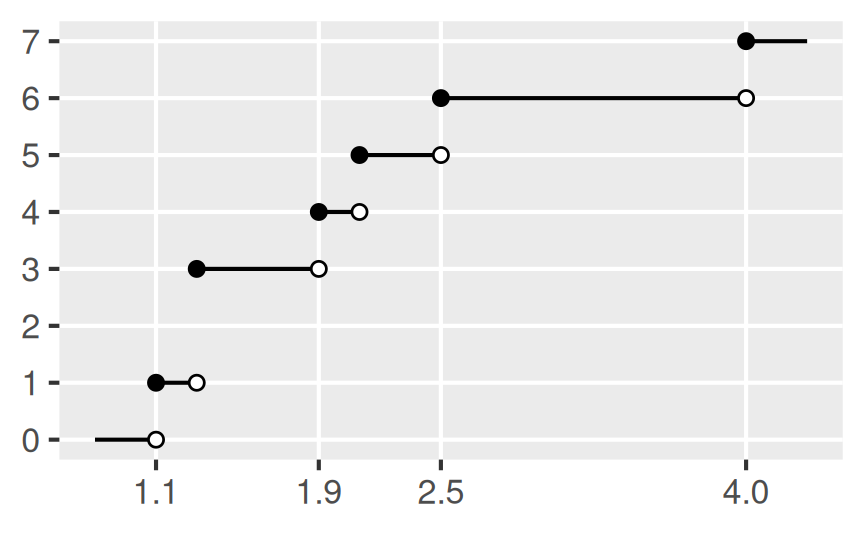
Am Graphen der absoluten kumulierten Häufigkeitsverteilung lässt sich nun unmittelbar ablesen, dass es (zum Beispiel) 4 Werte gibt, die kleiner oder gleich 1.9 sind.

Wie wir an dem Beispiel gesehen haben, ist die absolute Häufigkeitsverteilung \(H : \mathbb{R} \to \mathbb{N}\) also eine Funktion mit der Zuordnungsvorschrift

\[ H(x) = \text{'Anzahl der Werte $x_i$ mit $x_i \leq x$'} \]

beziehungsweise in mathematischer Schreibweise

\[ H(x) = h(a_1) + h(a_2) + \dots + h(a_j) = \sum_{i: ; a_i \leq x} h_i. \]

Dabei ist \(a_j\) die größte Ausprägung mit \(a_j \leq x\).

Empirische Verteilungsfunktion. In der Praxis wird meistens mit der empirischen Verteilungsfunktion oder der relative kumulierte Häufigkeitsverteilung gearbeitet. Diese Funktion wird mit \(F\) bezeichnet und gibt nicht die Anzahl der Ausprägungen an, die kleiner gleich dem Wert \(x\) sind, sondern den Anteil dieser Werte an der gesamten Stichprobe. Der Funktionswert ist daher

\[ F(x) = \text{'Anteil der Werte $x_i$ mit $x_i \leq x$' = H(x) / n} \]

beziehungsweise

\[ F(x) = f(a_1) + f(a_2) + \dots + f(a_j) = \sum_{i: \; a_i \leq x} f_i \]

wobei wieder \(a_j \leq x\) und \(a_{j+1} > x\) gelten soll.

Beispiel Klausurergebnisse (Fortsetzung ): Für die Mathematikklausur erhalten wir (mit den auf ganze Zahlen gerundeten Prozentpunkten) folgende empirische Verteilungsfunktion:

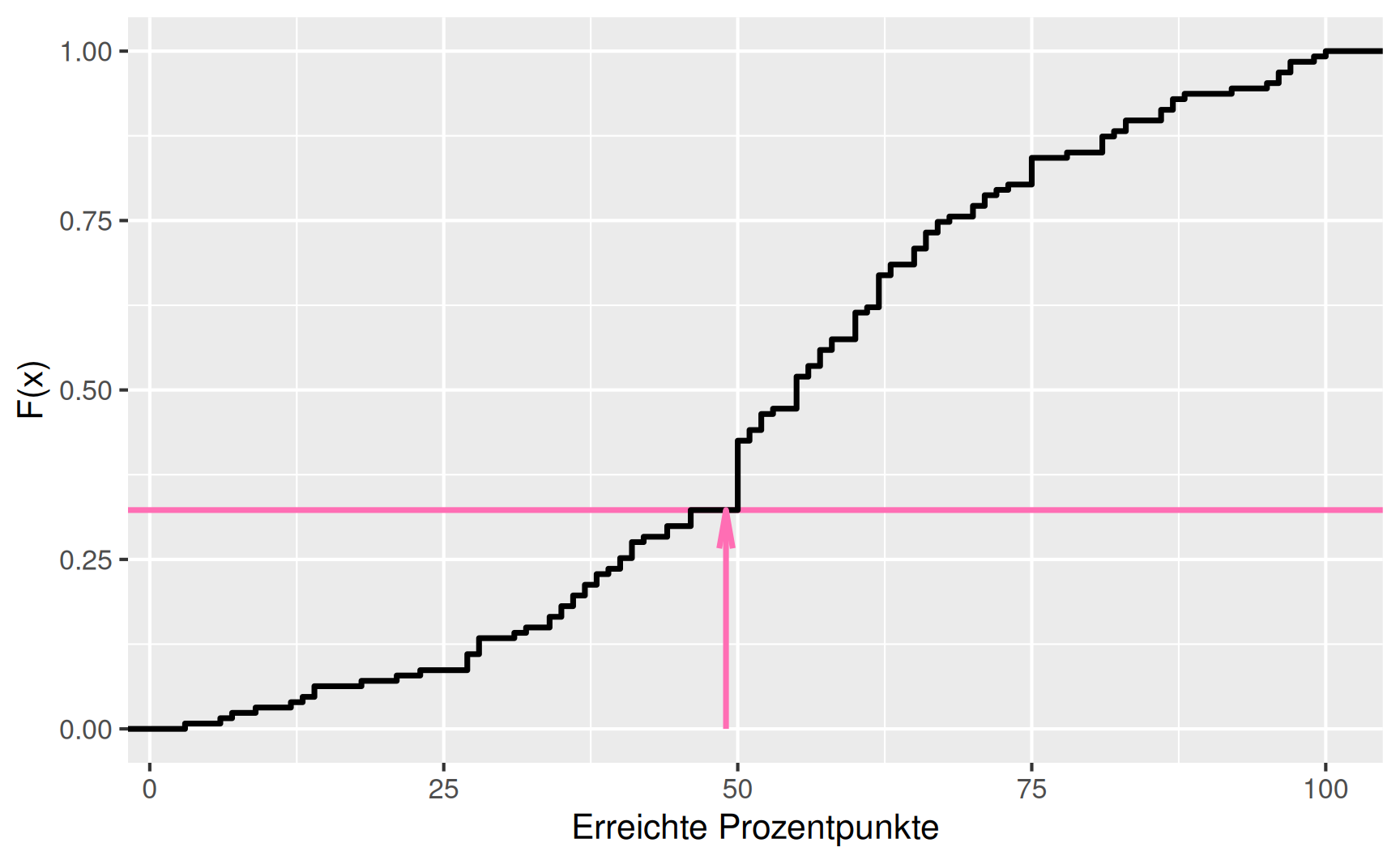
Beachten Sie, dass der Graph von \(F\) hier in Form einer Treppenfunktion dargestellt ist. Auf die Punkte, die den Funktionswert an einer Sprungstelle verdeutlichen, wird der Übersichtlichkeit halber verzichtet.

Die Durchfallquote bei der Klausur entspricht damit genau dem Funktionswert von \(F\) für \(x = 49\). Der Wert lässt sich mit dem Programm R einfach berechnen, es ist

\[ F(49) = 0.32 \]

und die Durchfallquote beträgt 32%.

Eigenschaften der Funktionen. Die Funktionen \(H\) und \(F\) haben folgende Eigenschaften:

• Beide Funktionen sind monoton wachsend.

• Für \(x < a_1\) ist der Funktionswert gleich null, es gilt also

  \[ H(x) = F(x) = 0 \quad \text{für} \quad x < a_1. \]

• Für \(x \geq a_k\) ist der Funktionswert von \(H\) gleich der Anzahl der Beobachtungen und für \(F\) gleich eins, so dass \[H(x) = n \quad \text{beziehungsweise} \quad F(x) = 1 \quad \text{für} \quad x \geq a_k\] gilt.

• Die Funktionen springen an den Stellen \(a_j\) jeweils um \(h_j\) beziehungsweise \(f_j\).