2  Statistische Daten

2.1 Datenquellen

Grundlage jeder statistischen Untersuchung sind Daten, die auf unterschiedliche Weise gesammelt oder gewonnen werden können. Zum Beispiel durch Umfragen (Wen würden Sie wählen, wenn am Sonntag Bundestagswahl wäre?), Zählungen (Wie viele Menschen steigen in einem bestimmten Zeitraum an der Haltestelle Lennershof aus der U35?), Messungen (Lufttemperatur und Luftdruck zu bestimmten Zeitpunkten), Versuchsreihen (Wie hoch ist die Bruchfestigkeit von Betonwürfeln?) oder durch Auswertungen protokollierter Daten (Suchwörter auf Google).

Heute sind viele Daten im Internet frei zugänglich. Hier einige Beispiele:

• Ministerien (etwa BMDV oder BMWK) und Bundesämter (Bundesanstalt für Straßenwesen, Statistisches Bundesamt).

• Das kostenpflichtige Statistik-Portal Statista. Die Hochschule Bochum hat eine Lizenz, aus dem Netz der Hochschule Bochum (von zu Hause aus über VPN) nutzbar.

• Die Berichte der Vereinten Nationen über die Entwicklung der Menschheit (Human Development Reports) http://hdr.undp.org

• Weltweite Wetterdaten des National Centers for Environmental Information der National Oceanic and Atmospheric Administration (US-Bundesbehörde) https://www.ncdc.noaa.gov/cdo-web/datasets

Wie Daten aus dem Bau- und Umweltingenieurwesen konkret aussehen können, sehen wir an folgenden Beispielen.

2.1.1 Beispiele aus dem Bau- und Umweltingenieurwesen

Mobilitätsbefragung – Wege zur BO

Im Rahmen des Moduls ‘Methoden der Verkehrsplanung’ von Prof. Mühlenbruch führen Studierende regelmäßig eine Befragung unter Angehörigen der BO durch. Ziel ist es herauszufinden, von wo und mit welchen Verkehrsmitteln die Befragten zur Hochschule gelangen. Auf Abbildung 2.1 links dargestellt ist der verwendete Fragebogen. Um die manuelle Übertragung der knapp 300 Fragebögen in eine Tabellenkalkulation zu vereinfachen sind Antworten mit Ziffern codiert. Entsprechend enthält die in Abbildung 2.1 rechts dargestellte tabellarische Zusammenfassung im Wesentlichen Zahlen und die Spaltenüberschriften sind etwas kryptisch.

Abbildung 2.1: Mobilitätsbefragung ‘Wege zur BO’ (Fragebogen und Auswertung)

Geschwindigkeitsmessung Universitätsstraße

Mit einem Seitenradar kann die Geschwindigkeit und die Länge der auf einer Straße vorbeifahrenden Fahrzeuge gemessen werden. Eine solche Messung ist von Prof. Mühlenbruch über zwei Tage im Jahr 2017 an der Universitätsstraße durchgeführt worden. Die Daten werden nach der Messung aus dem Messgerät ausgelesen und auf dem Computer in Form einer Excel-Datei gespeichert, siehe Abbildung 2.2.

Abbildung 2.2: Funktionsweise eines Seitenradars und aufgezeichnete Daten

Abfluss der Donau bei Hofkirchen

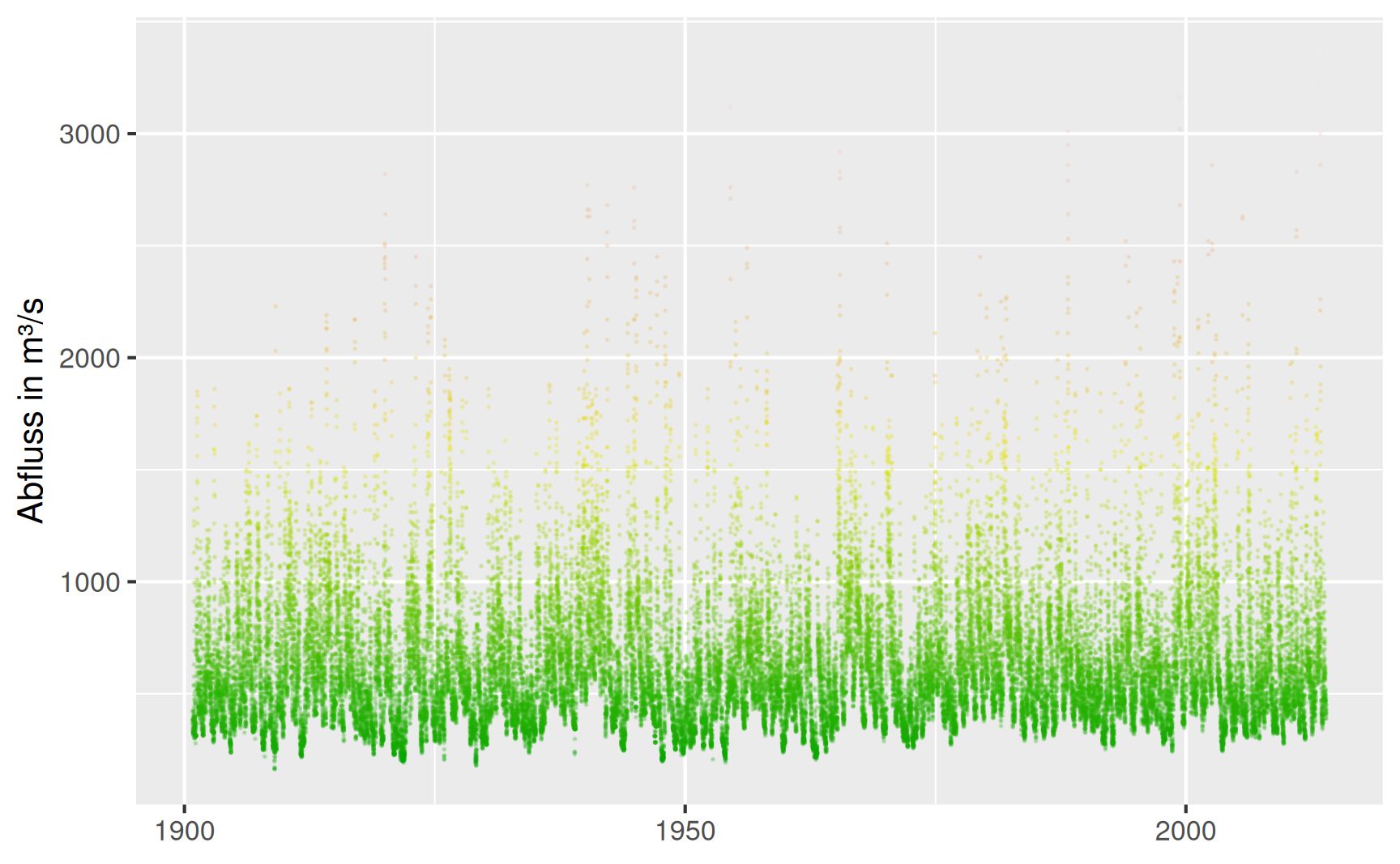
Historische Daten über den Abfluss und den Wasserstand eines Flusses bilden die Grundlage für die Beurteilung des Hochwasserrisikos und die Planung entsprechender Maßnahmen. Wir betrachten hier Messdaten der Donau am Pegel Hofkirchen, dargestellt in Abbildung 2.3. Es handelt sich um Messwerte des Abflusses in m³/s (Quelle: The Global Runoff Data Base der Bundesanstalt für Gewässerkunde. Die Daten mit einer Beobachtung pro Tag liegen in Textform vor, die einzelnen Werte sind durch Semikolons voneinander getrennt. Solche Dateien werden auch als CSV-Dateien bezeichnet (Comma Separated Values). Der Datensatz umfasst mehr als hundert Jahre und beinhaltet somit gut 40000 Werte.

Abbildung 2.3: Abfluss der Donau am Pegel Hofkirchen

2.2 Organisation von Datensätzen

In den Beispielen oben haben wir gesehen, in welcher Form Rohdaten vorliegen können. Um effizient statistische Untersuchungen durchführen zu können, ist es hilfreich, die Daten in einer gut handhabbaren Form zu darzustellen. Bei umfangreichen Daten geschieht das natürlich auf dem Computer. Die Entscheidung darüber, wie die einzelnen Werte angeordnet werden sollen, kann man dabei aber nicht dem Computer überlassen. Dass es hier durchaus Wahlmöglichkeiten gibt, sehen wir an dem folgenden Beispiel.

Beispiel: Wir betrachten einen fiktiven Datensatz zu Bevölkerungszahlen und das Auftreten von Krankheitsfällen in drei verschiedenen Ländern für die Jahre 1999 und 2000 (in Anlehnung an (Wickham und Grolemund 2016)). Nachfolgend dargestellt sind verschiedene Lösungen, wie die Daten in Tabellen zusammengestellt werden können.

Land	Jahr	Typ	Anzahl
Italien	1999	Fälle	745
Italien	1999	Bevölkerung	19987071
Italien	200	Fälle	2666
Italien	2000	Bevölkerung	20595360
Brasilien	1999	Fälle	37737
Brasilien	1999	Bevölkerung	172006362
Brasilien	2000	Fälle	80488
Brasilien	2000	Bevölkerung	174504898
China	1999	Fälle	212258
China	1999	Bevölkerung	1272915272
China	2000	Fälle	213766
China	2000	Bevölkerung	1280428583

Lösung 1: Eine Spalte mit Beschreibung, eine mit Werten

Land	Jahr	Fälle	Bevölkerung
Italien	1999	745	19987071
Italien	2000	2666	20595360
Brasilien	1999	37737	172006362
Brasilien	2000	80488	174504898
China	1999	212258	1272915272
China	2000	213766	1280428583

Lösung 2: Eine Spalte für jede Variable

Land	Jahr	Anteile
Italien	1999	745/19987071
Italien	2000	2666/20595360
Brasilien	1999	37737/172006362
Brasilien	2000	80488/174504898
China	1999	212258/1272915272
China	2000	213766/1280428583

Lösung 3: Kombination von Werten

Land	1999	2000
Italien	745	2666
Brasilien	37737	80488
China	212258	213766

Land	1999	2000
Italien	19987071	20595360
Brasilien	172006362	174504898
China	1272915272	1280428583

Lösung 4: Jeweils eine Tabelle für Fälle und Bevölkerung

Statistische Datensätze liegen in der Regel in Form rechteckiger Tabellen vor, die aus Zeilen und Spalten bestehen. Spalten sind dabei in der Regel mit einer Spaltenüberschrift versehen. Dabei hat es sich gezeigt, dass es häufig zielführend ist die Daten so aufzubereiten, dass die folgenden drei Anforderungen erfüllt sind:

1. Jede Variable erhält eine eigene Spalte

2. Jeder Beobachtung entspricht einer Zeile

3. Jeder Wert steht in einer eigenen Zelle

In Abbildung 2.4 ist zu erkennen, dass für das Beispiel oben mit Lösung 2 diesem Schema entsprochen wird.

Abbildung 2.4: Organisation eines Datensatzes in einer Tabelle

2.3 Statistische Grundbegriffe

2.3.1 Statistische Einheiten, Merkmale und Gesamtheiten

In diesem Abschnitt lernen wir einige in der Statistik übliche Begriffe kennen, die im Zusammenhang mit statistischen Datensätzen verwendet werden.

Statistische Einheit

In der Statistik wird meist davon ausgegangen, dass Daten an gewissen Objekten beobachtet werden. In unseren Beispielen:

• Student oder Studentin in der Mobilitätsbefragung

• Fahrzeug, das am Seitenradar vorbeifährt

Ein solches Objekt wird in der Statistik als statistische Einheit bezeichnet. Allerdings ist diese Vereinbarung nicht immer unproblematisch. Beispiele:

• Was ist die statistische Einheit in der Geschwindigkeitsmessung, wenn ein Fahrzeug innerhalb eines Messzeitraums zweimal am Seitenradar vorbeifährt?

• Bei der Durchflussmessung geht es immer um dasselbe Objekt, nämlich die Donau bei Hofkirchen.

Daher: Manchmal macht es Sinn, von statistischen Einheiten zu sprechen, den Begriff Beobachtung können wir aber immer verwenden.

Grundgesamtheit

Bei den in der Mobilitätsbefragung befragten Studierenden handelt es sich um eine Auswahl aller zum Zeitpunkt der Befragung an der BO eingeschriebenen Studierenden. Die Gesamtheit aller Studierenden bildet dabei die sogenannte Grundgesamtheit. Als Grundgesamtheit wird somit die Menge aller statistischen Einheiten bezeichnet, über die man Aussagen treffen möchte. In der Mobilitätsbefragung ist die Grundgesamtheit endlich groß und bekannt. Das ist nicht immer so:

• Die Geschwindigkeitsmessung lässt sich im Prinzip beliebig fortsetzen, es handelt sich hier um eine unendlich große Grundgesamtheit.

• Wenn man über die Abschlussnoten für Bauingenieursabsolventen der BO im Jahr 2095 nachdenkt, dann ist die Grundgesamtheit hypothetisch, da nicht bekannt ist, wer in Zukunft studieren wird.

Abbildung 2.5: Grundgesamtheit und Stichproben

Stichprobe

In den allermeisten Fällen ist es nicht möglich oder nicht notwendig in einer statistischen Untersuchung alle statistischen Einheiten der Grundgesamtheit einzubeziehen. Man beschränkt sich auf einen Teil der Grundgesamtheit und spricht dabei von einer Stichprobe . Abbildung 2.5 zeigt ein entsprechendes Beispiel.

Dass die Planung einer Erhebung keine triviale Aufgabe ist, sehen wir an zwei Beispielen:

• Abbildung 2.5 zeigt zwei Stichproben. Welche der beiden Stichproben können wir verwenden, um Aussagen über die Verteilung der Farben in der Grundgesamtheit zu treffen? Wie groß ist dann groß genug? Wir werden uns dieser Frage im Rahmen der schließenden Statistik zuwenden.

• Um eine aussagekräftige Stichprobe zu erhalten ist es notwendig, dass jede statistische Einheit mit gleicher Wahrscheinlichkeit in die Stichprobe aufgenommen wird. Wenn zum Beispiel die Befragung zur Mobilität auf dem Bahnsteig der U35 durchgeführt wird, dann ist die Stichprobe keinesfalls repräsentativ.

Für die Auswertung in einem Computerprogramm spielen diese Fragen keine Rolle. Hier entspricht die Stichprobe einfach dem statistischen Datensatz.

Merkmale

Eine Größe, für die man sich in einer statistischen Untersuchung interessiert, heißt Merkmal oder auch Variable. Manchmal betrachtet man nur ein einzelnes Merkmal (wie etwa den Abfluss des Pegels), in der Regel werden jedoch für eine einzelne statistische Einheit mehrere Merkmale erhoben. Die Merkmale können dabei für jede statistische Einheit unterschiedliche Werte annehmen (klar, sonst müsste man sie ja nicht erheben). Diese Werte werden auch Merkmalsausprägungen oder kurz Ausprägungen genannt.

Definition: Statistische Einheiten, Merkmale, Gesamtheiten

Statistische Einheiten:

Objekte an denen interessierende Größen erfasst werden

Grundgesamtheit:

Menge aller für die Fragestellung relevanten statistischen Einheiten

Stichprobe:

Tatsächlich untersuchte Teilmenge der Grundgesamtheit

Merkmal:

Interessierende Größe, Variable

Merkmalsausprägung:

Konkreter Wert für eine bestimmte statistische Einheit

2.3.2 Typen von Merkmalen

Für die statistische Auswertung von Daten ist es hilfreich und nützlich, Merkmale entsprechend bestimmter Eigenschaften in Kategorien einzuteilen. Dabei gibt es drei wesentliche Fragen:

1. Ist ein Merkmal stetig oder diskret?

2. Auf welcher Skala wird ein Merkmal gemessen?

3. Beschreibt das Merkmal eine Qualität oder eine Größe, die in Zahlen messbar ist?

Beachten Sie, dass diese Einordnungen nicht immer exakt gleich verwendet werden. Es handelt sich nicht um mathematische Definitionen sondern eher um eine Orientierungshilfe.

(a) Diskrete und stetige Merkmale

Eine wichtige Unterscheidung von Merkmalen betrifft die Anzahl möglicher Ausprägungen.

Diskret: Ein Merkmal heißt diskret, wenn es nur endlich viele oder abzählbar unendlich viele mögliche Ausprägungen gibt.

Stetig: Ein Merkmal heißt stetig, wenn es alle Werte eines Intervalls annehmen kann.

In der Regel ist es so, dass ausschließlich Merkmale, die sinnvollerweise durch reelle Zahlen repräsentiert werden, stetig sind. Alle anderen Merkmale sind diskret.

In der praktischen Anwendung werden stetige Merkmale durch Dezimalzahlen oder auch ganze Zahlen repräsentiert. In unserem Beispiel ist etwa die Körpergröße in ganzen Zentimetern erfasst. Obwohl das Merkmal stetig ist, haben wir es in der Auswertung mit diskreten Daten zu tun.

(b) Skalen von Merkmalen

Merkmale lassen sich auch nach der verwendeten Messskala klassifizieren. Es werden vier Skalenniveaus unterschieden.

1. Nominalskala: Ein Merkmal heißt nominalskaliert, wenn die Ausprägungen Namen oder Kategorien sind. Für Werte nominalskalierter Merkmale gibt es keine natürliche Rangfolge (im Sinn von besser, größer, schneller und so weiter).

2. Ordinalskala: Wenn es für die Ausprägungen eines Merkmals eine natürliche Ordnung gibt, es aber keinen Sinn macht, Abstände zwischen den Werten zu bestimmen, dann ist das Merkmal ordinalskaliert.

3. Intervallskala: Man spricht von einem intervallskalierten Merkmal, wenn die Ausprägungen

   1. Zahlen sind,

   2. sich die Differenz zwischen zwei Werten sinnvoll interpretieren lässt, es aber

   3. keinen natürlichen Nullpunkt gibt.

   Dadurch, dass es keinen Nullpunkt gibt, lassen sich keine Quotienten von Ausprägungen berechnen. Ein typisches Beispiel für eine intervallskalierte Größe ist die Temperatur in Grad Celsius: Die Aussage

   “Gestern Mittag waren es 10° C, heute sind es 20°C. Es ist also doppelt so warm.’’

   macht wenig Sinn.

4. Verhältnisskala: Gibt es für ein zahlenwertiges Merkmal zusätzlich noch einen natürlichen Nullpunkt, dann lassen sich Quotienten bilden und man spricht von einem verhältnisskalierten Merkmal. Zum Beispiel gibt es für die Geschwindigkeit einen natürlichen Nullpunkt und der Satz

   “Mein Porsche fährt mehr als doppelt so schnell wie dein Smart’’

   ist sinnvoll, auch wenn man sich über ein allgemeines Tempolimit durchaus streiten kann.

Intervall- und Verhältnisskalen werden unter den Oberbegriffen Kardinalskala oder metrische Skala zusammengefasst. In der folgenden Tabelle sind Skalenarten und zugehörige sinnvolle Operationen nochmals kompakt dargestellt.

Skalenart	auszählen	ordnen	Differenzen bilden	Quotienten bilden
nominal	Ja	Nein	Nein	Nein
ordinal	Ja	Ja	Nein	Nein
Intervall	Ja	Ja	Ja	Nein
Verhältnis	Ja	Ja	Ja	Ja

(c) Qualitative und quantitative Merkmale

Eine weiterer Aspekt nach dem Merkmale unterschieden werden können, betrifft den Typ der Merkmalsausprägung: Handelt es sich um eine Kategorie oder um eine Größe, die in Zahlen messbar ist.

1. Qualitative Merkmale: Wenn ein Merkmal endlich viele Ausprägungen besitzt und nominal- oder ordinalskaliert ist, dann nennt man es ein qualitatives Merkmal. Wesentlich dabei ist, dass die Ausprägungen einer Qualität oder einer Kategorie entspricht.

2. Quantitative Merkmale: Lässt sich ein Merkmal auf einer Intervall- oder Verhältnisskala messen, dann spricht man von einem quantitativen Merkmal. Eine Ausprägung ist hier eine Zahl, die eine Menge, Intensität oder ein Ausmaß wiedergibt.

Anmerkung: Es gibt auch Merkmale, die weder qualitativ noch quantitativ sind, zum Beispiel Eigennamen.

In der Folgenden Definition sind die Arten von Merkmalen nochmals kompakt zusammengefasst.

Definition: Arten von Merkmalen

Diskret:

endlich oder abzählbar unendlich viele Ausprägungen

Stetig:

alle Werte eines Intervalls, Werte sind reelle Zahlen

Nominalskaliert:

Ausprägungen sind Namen, keine Reihenfolge

Ordinalskaliert:

Ausprägungen lassen sich ordnen, Abstände nicht interpretierbar

Intervallskaliert:

Ausprägungen sind Zahlen, Abstände sinnvoll interpretierbar

Verhältnisskaliert:

Wie intervallskaliert, aber mit absolutem Nullpunkt

Qualitativ:

endlich viele Ausprägungen, nominal- oder ordinalskaliert

Quantitativ:

als Zahlenwert messbar

Wickham, H., und G. Grolemund. 2016. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. O’Reilly Media. http://r4ds.had.co.nz.