4  Fehlerrechnung

 

“Das Experimentieren ist ein dornenvoller Weg und so ganz sicher ist man sich nie.”

 

Wagner, Paul. 2015. “Einführung in die Physik I. PH I - 04 - Die Messgenauigkeit / Fehlerrechnung Teil 1.” Universität Wien Physik, YouTube, Zeitstempel 04:05

 

Kein Messgerät misst exakt und nicht alle Umwelteinflüsse können kontrolliert werden. Das Ziel der Fehlerrechnung ist es, die sich daraus ergebende Abweichung der Messwerte um den wahren Wert einer Größe zu quantifizieren.

4.1 Bevor es losgeht

Das Thema ist jedoch mit einigen Schwierigkeiten verbunden, die den Einstieg und die eigenständige Vertiefung des Themas erschweren.

Der Begriff des Fehlers

Das Wort Fehler steckt zwar schon in der Überschrift dieses Kapitels, doch handelt es sich seit 1995 nicht mehr um einen genormten Begriff. Die DIN 1319 normt Grundbegriffe und Verfahren der Messtechnik. Die Norm ersetzt den Begriff des Fehlers durch die Begriffe Messabweichung und Messunsicherheit, umfasst aber darüber hinaus eine Vielzahl aufeinander bezogener Begriffsdefinitionen, Anmerkungen und Bemerkungen.

In diesem Kapitel werden die in der Fehlerrechnung gebräuchlichen Begriffe aufgegriffen, um die Verbindung zu den genormten Begriffen herzustellen. Im Allgemeinen werden jedoch die genormten Begriffe verwendet. Um den Einstieg in das Thema zu erleichtern, beschränkt sich dieses Kapitel auf Messungen mit:

• unkorrelierten Eingangsgrößen und
• vernachlässigbarer Unsicherheit über die systematische Messabweichung.

Konfidenzniveau

Wiederholte Messungen enthalten eine zufällige Komponente statistischer Unsicherheit. Die statistische Unsicherheit kann immer nur mit einer Vertrauenswahrscheinlichkeit angegeben werden. Die Berechnung von Konfidenzintervallen haben wir in Kapitel 2 und Kapitel 3 behandelt.

Zur statistischen Analyse gehört als erster Schritt, das Konfidenzniveau, das gelten soll, festzulegen. Hieraus leiten sich die zu verwendenden Vielfachen der Standardabweichung \(s\) bzw. des Korrekturfaktors \(t\) ab. Hierbei gibt es je nach Disziplin unterschiedliche Konventionen.

 

“In der Physik und der Vermessungstechnik begnügt man sich mit einer statistischen Sicherheit von 68,3% und setzt deshalb t = 1 […] (In der Industrie wird t = 2, in der Biologie t = 3 bevorzugt.)” (Hochschule Aalen 2016, 4)

 

In der ingenieurswissenschaftlichen Literatur wird dieser Schritt nicht immer explizit gemacht (weil es üblich ist, \(1 s\) bzw. \(1 t\) zu verwenden). Dagegen heißt es in der DIN 1319: “Es ist üblich, das Vertrauensniveau (\(1 - \alpha\)) in Prozent anzugeben, wobei meist \(\alpha = 0,05\) (Vertrauensniveau: 95 %) benutzt wird.” (Deutsches Institut für Normung 1995, 17)

Notation

Die Notation ist komplex: Neben dem lateinischen und griechischen Alphabet wird auch das kyrillische Alphabet verwendet. Trotzdem lassen sich Dopplungen von Symbolen für Formelzeichen und Einheiten nicht immer vermeiden (und die Federkonstante ist in dieser Hinsicht der denkbar ungünstigste Fall).

Die Notation wird außerdem uneinheitlich gehandhabt. Während in der DIN 1319 Messabweichungen mit \(e\) notiert werden, sind in der Literatur \(\epsilon\) (epsilon) und \(\Delta\) (Delta) gebräuchlich, wobei letzteres auch für den Größtfehler verwendet wird.

Übrigens: Das in der DIN verwendete \(e\) steht für error, also Fehler ( ¯\_(ツ)_/¯ ).

4.2 Fehlerarten

Bei Messungen können unterschiedliche Arten von Abweichungen des Messergebnisses vom tatsächlichen Wert der gemessenen Größe auftreten. Am gebräuchlichsten ist die Unterteilung in grobe, systematische und zufällige Fehler. Nach DIN 1319 sollte besser von systematischen und zufälligen Messabweichungen gesprochen werden. Grobe Fehler werden in der Norm jedoch nicht behandelt und hier ist der Fehlerbegriff durchaus angemessen.

• Systematische Messabweichungen: unter identischen Bedingungen konstante, d. h. nach Betrag und Vorzeichen gleiche, Verzerrung der Messergebnisse durch Abweichungen der Messgeräte. Beispielsweise:

  • in Abhängigkeit von der Temperatur
  • fehlerhafte Kalibrierung
  • Alterung der Bauteile
  • die Art der Messung, z. B. Ablese- und Skalenfehler, Messintervall bei digitalen Messgeräten (Quantifizierungsfehler)

• Zufällige Messabweichungen: statistische Streuung der Messwerte um ihren Erwartungswert. Beispielsweise:

  • Stichprobenfehler
  • Ablesefehler

• Grobe Fehler: Verfälschen der Messergebnisse. Beispielsweise durch:

  • falschen Versuchsaufbau
  • ungeeignete Messgeräte
  • falsches Ablesen, z. B. Missachtung der Einschwingzeit oder Unachtsamkeit, z. B. Mitwiegen des Gefäßes

(Hempel 2016, 1–2; Eden und Gebhard 2024, 17–18)

Bestimmte Tätigkeiten, wie das Ablesen, können mehreren Fehlerarten zugehörig sein:

• Unaufmerksames Ablesen und Flüchtigkeitsfehler sind grobe Fehler,
• winkel- und positionsabhängige Fehler wie der Parallaxenfehler sind systematische Abweichungen,
• Fehler infolge des begrenzten Auflösungsvermögens des menschlichen Auges führen zu zufälligen Abweichungen.

Tipp 4.1: Umgang mit verschiedenen Arten von Messabweichungen

1. Grobe Fehler: Betroffene Werte streichen und Messung wiederholen.

2. Systematische Messabweichungen: Systematische Messabweichungen werden, wenn sie bekannt sind, korrigiert.

3. Zufällige Messabweichungen: Die statistische Streuung von Messwerten um den Erwartungswert wird quantifiziert.

Einige systematische und zufällige Messabweichungen können nur mit hohem Aufwand reduziert werden (genauere Messgeräte, größere Anzahl von Messvorgängen). Der Aufwand muss gegen den Gewinn an Genauigkeit abgewogen werden: Ist das Messergebnis mit der angegebenen Unsicherheit akzeptabel?

(Hempel (2016), S. 2)

4.3 Grundbegriffe nach DIN 1319

Die DIN 1319 normt Grundbegriffe und Verfahren der Messtechnik.

• Teil 1 DIN 1319-1 und Teil 2 DIN 1319-2 definieren Grundbegriffe der Messtechnik und für Messmittel.
• Teil 3 DIN 1319-3 befasst sich mit der Auswertung von Messungen einer einzelnen Messgröße und deren Messunsicherheit. DIN 1319-3 wird auch angewendet, wenn die Meßgröße mittels einer gegebenen Funktion aus anderen Größen berechnet wird (beispielsweise die Geschwindigkeit \(v\) als Quotient der Strecke \(s\) und der Zeit \(t\)).
• Teil 4 DIN 1319-4 befasst sich mit der Angabe von Messergebnissen und deren Messunsicherheit, wenn die Messgrößen aus anderen Größen berechnet werden, z. B. durch eine Ausgleichsrechung.

DIN 1319-4 befasst sich mit der Berechnung einer Ergebnisgröße \(Y\) durch eine Funktion wie z. B. die lineare Ausgleichsrechnung. Der Anwendungsfall des vorherigen Kapitels, die Federkonstante über den Regressionskoeffizienten \(\beta_1\) zu bestimmen, wird in der Norm nicht behandelt. Dieser Teil der Norm wird hier deshalb nicht vorgestellt.

Das Lernziel dieses Kapitels besteht darin, dass Sie die folgende Grafik aus der DIN 1319 erklären können.

Messergebnis nach DIN 1319

(Deutsches Institut für Normung 1995, 30)

 

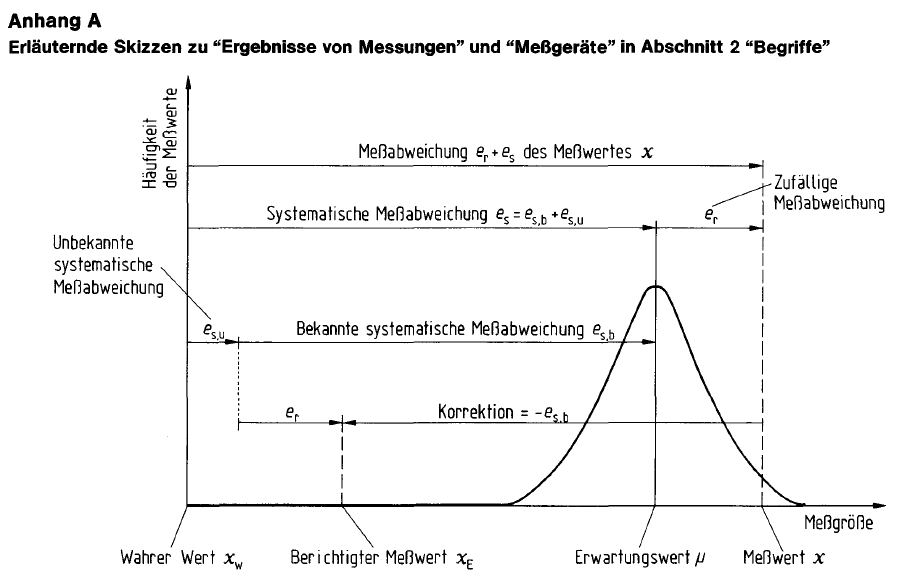
Die drei wichtigsten Grundbegriffe sind:

1. Messabweichung,
2. Messunsicherheit und
3. vollständiges Messergebnis.

Messabweichung

Der in der Fehlerrechnung gebräuchliche Begriff des (Mess-)Fehlers meint im engeren Sinn die Messabweichung nach DIN 1319, also die tatsächliche Abweichung eines einzelnen Messwerts oder des arithmetischen Mittelwerts einer Messreihe (dem unberichtigten Messergebnis) vom wahren Wert der gemessenen Größe.

Definition 4.1: Messabweichung nach DIN 1319

Die Messabweichung ist die: “Abweichung eines aus Messungen gewonnenen und der Meßgröße […] zugeordneten Wertes vom wahren Wert […]. Ist \(m\) der der Meßgröße zugeordnete Wert und \(x_w\) der wahre Wert, so ist die Meßabweichung des zugeordneten Wertes \(m - x_w\) […].” (Deutsches Institut für Normung 1995, 12)

Die Messabweichung des unberichtigten Messergebnisses setzt sich additiv aus der zufälligen Messabweichung \(e_r\) und der systematischen Messabweichung \(e_s\) zusammen.

• Die systematische Messabweichung ist die Differenz aus dem Erwartungswert der Messung \(\mu\) und dem wahrem Wert \(x_w\). Es gilt: \(e_s = \mu - x_w\)
  
• Die systematische Messabweichung \(e_s\) setzt sich aus einem bekannten \(e_{s,b}\) und einem unbekannten Anteil \(e_{s,u}\) zusammen.
• Die bekannte, systematische Messabweichung \(e_{s,b}\) wird mit entgegengesetzten Vorzeichen \(- e_{s,b}\) Korrektion genannt.

Das (berichtigte) Messergebnis \(\bar{x}_E\) ist das um die bekannte, systematische Messabweichung \(e_{s,b}\) berichtigte arithmetische Mittel einer Messreihe \(\bar{x}\), das als Schätzer des wahren Werts \(x_w\) verwendet wird. \(\bar{x}_E = \bar{x} - e_{s,b}\)

(Deutsches Institut für Normung 1995, 11–13)

Messunsicherheit

Der wahre Wert einer gemessenen Größe ist in der Regel unbekannt, sodass die tatsächliche Messabweichung ebenfalls nicht bekannt ist. Deshalb kann nur eine aus den Messgrößen gewonnene Schätzung der Messabweichung - die Messunsicherheit - angegeben werden. Der in der Fehlerrechnung gebräuchliche Begriff des (Mess-)Fehlers meint im weiteren Sinn die Messunsicherheit nach DIN 1319.

Definition 4.2: Messunsicherheit nach DIN 1319

“Kennwert, der aus Messungen […] gewonnen wird und zusammen mit dem Meßergebnis […] zur Kennzeichnung eines Wertebereiches für den wahren Wert der Meßgröße […] dient.” (Deutsches Institut für Normung 1995, 14, eigene Hervorhebung)

Während die Messabweichung ein Einzelwert ist, kennzeichnet die Messunsicherheit einen Wertebereich: “Die Meßunsicherheit ist von der Meßabweichung […] deutlich zu unterscheiden. Letztere ist nur die Differenz zwischen einem der Meßgröße zuzuordnenden Wert […] und dem wahren Wert. Die Meßabweichung kann gleich Null sein, ohne daß dies bekannt ist. Diese Unkenntnis drückt sich in einer Meßunsicherheit größer als Null aus.” (Deutsches Institut für Normung 1996, 3)

Die Messunsicherheit einer Messgröße \(Y\) besteht einerseits aus der zufälligen Messabweichung \(e_r\) und andererseits aus der Unsicherheit über die systematische Messabweichung \(u(e_s)\).

zufällige Messabweichung

Wird eine Messgröße \(Y = y(x)\) durch mehrere, direkte Messungen bestimmt, so streuen die Messwerte \(x_i\) zufällig um ihren Erwartungswert \(\mu\) mit der Standardabweichung \(\sigma\). Der Erwartungswert \(\mu\) und die Standardabweichung \(\sigma\) sind in der Regel nicht bekannt und werden aus den Messwerten durch den arithmetischen Mittelwert \(\bar x\) und die empirische Standardabweichung \(s_{n-1}\) geschätzt. (siehe Kapitel 1)

Als Unsicherheit der zufälligen Streuung wird die empirische Standardabweichung des Mittelwerts verwendet.

\[ u(\bar x) = \frac{s_{n-1}}{\sqrt{N}} ~ = ~ \sqrt{\frac{1}{N(N-1)} \sum_{i=1}^{N}(x_i - \bar{x})^2} \]

(Deutsches Institut für Normung 1996, Gleichung (4), S. 5, Notation angepasst)

systematische Messabweichung

Die systematische Messabweichung \(e_s\) setzt sich aus einem bekannten Anteil \(e_{s,b}\) und einem unbekannten Anteil \(e_{s,u}\) zusammen. Da der unbekannte Anteil nicht bestimmt werden kann, wird die gesamte systematische Messabweichung über die bekannte systematische Messabweichung \(e_{s,b}\) geschätzt. Daraus ergibt sich eine Unsicherheit über die tatsächliche gesamte systematische Messabweichung \(u(e_{s})\). Diese Unsicherheit besteht auch, wenn die bekannte systematische Messabweichung \(e_{s,b}\) Null ist, weil der unbekannte Anteil \(e_{s,u}\) ungleich Null sein kann.

In der DIN 1319 werden zwei Fälle unterschieden, je nachdem, ob die Unsicherheit \(u(e_{s})\) als vernachlässigbar eingeschätzt wird oder nicht. In diesem Kapitel gehen wir von einer vernachlässigbaren Unsicherheit \(u(e_{s})\) aus (Für den zweiten Fall siehe Beispiel).

Beispiel 4.1: \(u(e_{s})\) nicht vernachlässigbar

Für den Fall, dass die Unsicherheit der systematischen Messabweichung nicht als vernachlässigbar angesehen wird, verweist die DIN 1319-3 auf Berechnungsregeln in Abschnitt 6.2.5 auf die wir hier nicht eingehen. (Deutsches Institut für Normung (1996), S. 5-6)

Die Messunsicherheit des berichtigten Messergebnisses berechnet sich aus der quadratischen Kombination der Unsicherheiten der zufälligen und der systematischen Messabweichung.

\[ u(y) = \sqrt{u^2(\bar x) + u^2(e_s)} \]

(Deutsches Institut für Normung 1996, Gleichung (8), S. 6, Notation angepasst)

Hinweis 4.1: Notation in der DIN 1319

In der DIN wird die zufällige Messabweichung statt mit \(u^2(\bar x)\) mit \(u^2(x_1)\) und die Unsicherheit der systematischen Messabweichung statt mit \(u^2(e_s)\) mit \(u^2(x_2)\) notiert.

Vollständiges Messergebnis

Das berichtigte Messergebnis \(\bar{x}_E = y\) (in der DIN 1319 wechselt die Notation von \(\bar{x}_E\) zu \(y\)) berechnet sich durch die Korrektion der bekannten systematischen Messabweichung:

\[ y = \bar x - e_{s,b} \]

(Deutsches Institut für Normung 1996, Gleichung (7), S. 6, Notation angepasst)

Das vollständige Messergebnis \(Y\) besteht aus dem berichtigten Messergebnis und einer Angabe über die Unsicherheit der Messung z. B. in der Form:

\[ Y = y \pm u(y) \]

(Deutsches Institut für Normung 1996, Gleichung (9), S. 6)

Zusätzlich zum vollständigen Messergebnis kann ein Vertrauensbereich (auch: Vertrauensintervall oder Konfidenzintervall) angegeben werden. Der Berechnung von Konfidenzintervallen haben wir im Kapitel Kapitel 2 vorgegriffen.

\[ y - t \cdot u(y) \le Y \le y + t \cdot u(y) \]

(Deutsches Institut für Normung 1996, Gleichung (14), S. 7)

Die Wahl eines Vertrauensbereichs ist Ermessenssache. Die DIN 1319 formuliert dazu: “Es ist üblich, das Vertrauensniveau (\(1 - \alpha\)) in Prozent anzugeben, wobei meist \(\alpha = 0,05\) (Vertrauensniveau: 95 %) benutzt wird.” (Deutsches Institut für Normung 1995, 17) “Dieses Vertrauensniveau von 95 % sollte verwendet werden, aber kein höheres.” (Deutsches Institut für Normung 1996, 7)

So ergibt sich beispielsweise:

\[ y - t_{\alpha / 2} \cdot \frac{s_{n-1}}{\sqrt{n}} \le Y \le y + t_{\alpha / 2} \cdot \frac{s_{n-1}}{\sqrt{n}} \]

Hinweis 4.2: Notation in der DIN 1319

In der DIN wird der arithmetische Mittelwert einer Messreihe statt mit \(\bar{x}\) mit \(\bar{v}\) notiert.

Übersicht

In der DIN 1319 werden eine Reihe weiterer Begriffe definiert, die im folgenden Kasten zusammen mit den wichtigsten Grundbegriffen zusammengestellt wurden.

Definition 4.3: Grundbegriffe nach DIN 1319

Messabweichung: “Abweichung eines aus Messungen gewonnenen und der Meßgröße […] zugeordneten Wertes vom wahren Wert […]. Ist \(m\) der der Meßgröße zugeordnete Wert und \(x_w\) der wahre Wert, so ist die Meßabweichung des zugeordneten Wertes \(m - x_w\) […].” (Deutsches Institut für Normung 1995, 12)

• Die Messabweichung des unberichtigten Messergebnisses setzt sich additiv aus der zufälligen Messabweichung \(e_r\) und der systematischen Messabweichung \(e_s\) zusammen.
• Die systematische Messabweichung \(e_s\) setzt sich aus einem bekannten \(e_{s,b}\) und einem unbekannten Anteil \(e_{s,u}\) zusammen.
• Die systematische Messabweichung ist die Differenz aus Erwartungswert \(\mu\) und wahrem Wert \(x_w\). \(e_s = \mu - x_w\)
• Die bekannte, systematische Messabweichung \(e_{s,b}\) wird mit entgegengesetzten Vorzeichen \(- e_{s,b}\) Korrektion genannt.

Das Messergebnis \(\bar{x}_E\) ist das um die bekannte, systematische Messabweichung \(e_{s,b}\) berichtigte arithmetische Mittel einer Messreihe \(\bar{x}\), das als Schätzer des Erwartungswerts \(\mu\) verwendet wird.
\(\bar{x}_E = \bar{x} - e_{s,b}\)

(Deutsches Institut für Normung 1995, 11–13)

Messunsicherheit \(u\) oder \(u(y)\): “Kennwert, der aus Messungen […] gewonnen wird und zusammen mit dem Meßergebnis […] zur Kennzeichnung eines Wertebereichs für den wahren Wert der Meßgröße […] dient.” (Deutsches Institut für Normung 1995, 14)

• Standardmessunsicherheit oder kurz Standardunsicherheit wird verwendet, wenn die Messunsicherheit durch eine Standardabweichung ausgedrückt wird. (Deutsches Institut für Normung 1996, 3)

• erweiterte Messunsicherheit \(U(y) = k \cdot u(y)\): Wertebereich, der den wahren Wert der Messgröße wahrscheinlich enthält. Der Erweiterungsfaktor \(k\) sollte zwischen 2 und 3 festgelegt werden, vorzugsweise wird \(k = 2\) verwendet. Der Erweiterungsfaktor \(k\) ist mitzuteilen, damit die Standardmessunsicherheit \(u(y) = U(y) / k\) ermittelt werden kann. (Deutsches Institut für Normung 1996, 7)
  Hinweis: Die erweiterte Messunsicherheit unterscheidet sich vom Konfidenzintervall dadurch, dass keine Normalverteilung unterstellt wird - es ist schlicht ein Faktor, ‘um auf Nummer sicher zu gehen’, dass der wahre Wert vom angegebenen Bereich eingeschlossen wird.

Das vollständige Messergebnis ist das Messergebnis mit quantitativen Angaben zur Messunsicherheit \(u\). \(x = \bar{x}_E \pm u\). (Deutsches Institut für Normung 1995, 16)

• Der Vertrauensbereich \(\bar x - t \cdot u(y) \le Y \le y + t \cdot u(y)\) kann zusätzlich zum vollständigen Messergebnis angegeben werden.

  • Ist die systematische Messabweichung bekannt und korrigiert worden, dann liegt der wahre Wert der Messgröße \(Y\) innerhalb des Vertrauensbereichs.
  • Wenn die systematische Messabweichung nicht bekannt ist, liegt der Erwartungswert \(\mu\) der Verteilung im Vertrauensbereich. (Deutsches Institut für Normung 1996, 7)

  Hinweis: In der DIN wird der arithmetische Mittelwert einer Messreihe statt mit \(\bar{x}\) mit \(\bar{v}\) geschrieben.

4.4 Absolute und relative Fehler

In der Fehlerrechnung werden absolute und relative Fehler unterschieden. Hier sollte besser von absoluter und relativer Messunsicherheit gesprochen werden.

• Die absolute Messunsicherheit \(u\) wird in der Einheit der gemessenen Größe angegebenen: \(u(m) = 0,2 kg\). Das vollständige Messergebnis lautet: \(m = 5,0 \pm 0,2 kg\) oder \(m = 5,0 kg \pm 0,2 kg\).

• Die relative Messunsicherheit \(u_{rel}(m) = \frac{u(m)}{ | m | }\) wird entweder als Produkt in der Form \(m \cdot (1 \pm \frac{u(x)}{| m |})\) angegeben. Bspw.:

  \(m = 5,0 kg \cdot (1 \pm \frac{0,2 kg}{5,0 kg}) = 5,0 kg \cdot (1 \pm 0,04)\)

  Alternativ wird die relative Messunsicherheit in Prozent \(u_{rel}(m) = \frac{u(m)}{| m |} \cdot 100 ~ \%\) angegeben. Bspw.:

  \(m = 5,0 kg \pm 4 ~ \%\).

(Deutsches Institut für Normung 1995, 9–10, 16; 1996, 10)

Hinweis 4.3: (Alternative) Notationen

In der DIN 1319 werden Messabweichungen mit \(e\), die Messunsicherheit mit \(u\) notiert. In der Literatur zur Fehlerrechnung wird zumeist der Begriff des (Mess-)Fehlers verwendet. Die Notation ist allerdings uneinheitlich.

• Der absolute Fehler wird häufig mit \(\epsilon x\) (epsilon x) notiert. Üblich ist aber auch die Notation mit \(\Delta x\) (Delta), (beispielsweise (Hochschule Aalen 2016; Dinter, Ralf 2011; Schrüfer, Reindl, und Zagar 2022). \(\Delta\) wird aber ebenfalls für den Größtfehler verwendet.

• Der relative Fehler wird auch mit \(\delta x\) (delta x) notiert, bspw: \(\delta x = 4 \%\).

4.5 Größtfehler

Systematische Messabweichungen \(e(x)_{s}\) bewirken eine einseitige Verzerrung des Messergebnisses, sodass der Messwert immer zu hoch oder zu niedrig ausfällt. Zufällige Messabweichungen \(e(x)_{r}\) führen unkontrolliert mal zum Über-, mal zum Unterschätzen des Messwerts.

In der Regel werden sich die verschiedenen Messabweichungen teilweise ausgleichen. Als Größtfehler wird der ungünstigste Fall bezeichnet, bei dem sich alle Messabweichungen jeweils um ihren maximalen (oder minimalen) Wert gegenseitig verstärken, sodass der Messwert die maximal mögliche Abweichung vom (unbekannten) tatsächlichen Wert aufweist. Der Größtfehler wird als \(\Delta x\) (Delta x) notiert.

Der Größtfehler einer Messreihe für eine Größe wird ermittelt, indem man die Beträge der einzelnen Messabweichungen addiert.

\[ \Delta x = | e(x)_{s} | + | e(x)_{r} | \]

Da Messungen bei groben Fehlern als ungültig anzusehen sind, entfällt der Anteil grober Fehler \(| e(x)_{grob} |\).

(Eden und Gebhard (2024), S. 35-36)

Werden mehrere Größen betrachtet, addieren sich die Größtfehler der beteiligten Größen zum Größtfehler der Ergebnisgröße. So gilt für eine Größe \(Y = f(x_1, x_2)\): \[ \Delta y = \Delta x_1 + \Delta x_2 \]

Tipp 4.2: Größtfehler

Der Größtfehler ist keine genormte Angabe nach DIN 1319, sondern eine vereinfachte Form der Fehlerabschätzung und überschätzt die wahrscheinliche Messunsicherheit.

“Für viele Betrachtungen, speziell in den Grundlagenpraktika der ersten Semester in technischen, naturwissenschaftlichen und ingenieurmäßigen Studiengängen, reicht es aus, den maximalen Fehler (absoluter Größtfehler) zu bestimmen.” (Eden und Gebhard (2024), S. 35)

4.6 Signifikante Stellen

Bei der Angabe des vollständigen Messergebnisses ist die Anzahl der signifikanten oder zuverlässig bekannten Stellen zu beachten.

Definition 4.4: signifikante Stellen

“Jede zuverlässig bekannte Stelle mit Ausnahme der Nullen, die die Position des Dezimalkommas angeben, wird signifikante Stelle genannt.” (Eden und Gebhard 2024, 24)

“Gerundete numerische Unsicherheitwerte sind mit zwei (oder bei Bedarf mit drei) signifikanten Ziffern anzugeben. Sie sind aufzurunden. Das Meßergebnis ist an derselben Stelle wie die zugehörige Unsicherheit zu runden, z.B. \(y = 245,5716 mm\) auf \(y = 245,57 mm\), wenn \(u(y) = 0,4528 mm\) auf \(u(y) = 0,46 mm\) aufgerundet wird.” (Deutsches Institut für Normung 1996, 6, eigene Hervorhebung)

Beispielsweise liegen die im vorherigen Kapitel verwendeten Abstandsmessungen im Format \(153,29\) vor, die Messwerte weisen also 5 signifikante Stellen auf. Für den arithmetischen Mittelwert einer Messreihe \(153,008889\) gelten deshalb ebenfalls 5 signifikante Stellen. Es wird an der ersten nicht mehr signifikanten Stelle gerundet, sodass der arithmetische Mittelwert mit \(153,01\) angegeben wird.

Die Anzahl signifikanter Stellen ist allerdings nicht immer zuverlässig zu bestimmen. Es gilt:

1. Alle Ziffern ungleich Null sind immer signifikant.
2. Führende Nullen sind niemals signifikante Stellen. Beispielsweise hat 0012 km 2 signifikante Stellen. 0,001 mm hat eine signifikante Stelle.
3. Nullen am Ende einer Zahl sind signifikant, wenn sie sich rechts vom Dezimaltrennzeichen befinden, bspw: 12,100 km hat 5 signifikante Stellen.
4. Nullen, die sich am Ende einer Zahl ohne Komma befinden, können signifikant sein. 1200 m kann zwei oder vier signifikante Stellen haben.

signifikante Stellen und wissenschaftliches Runden

Angaben zur Messunsicherheit werden zwar aufgerundet. Trotzdem an dieser Stelle: Kennen Sie den Unterschied zwischen kaufmännischem und wissenschaftlichem Runden?

Runden und signifikante Stellen (Vorkurs Mathematik) von Edmund Weitz ist abrufbar auf YouTube. 2019

Python rundet wissenschaftlich:

print(round(2.5), round(3.5))

2 4

4.7 Methoden der Fehlerrechnung

Das Ziel der Fehlerrechnung ist es, Unsicherheitsintervalle für die gemessene Größe zu ermitteln. Dafür stehen verschiedene Methoden zur Verfügung:

1. Fehlerabschätzung,
2. Fehlerstatistik und
3. Fehlerfortpflanzung.

Bei der Auswahl der Methode besteht ein Ermessensspielraum. (Hempel (2016), S. 2) Für Gebrauchsmessungen reicht es aus, die Unsicherheit im Prozentbereich anzugeben. Im Eichwesen oder beim Vergleich mit einem Normal werden genauere Angaben benötigt. (Schrüfer, Reindl, und Zagar 2022, 33)

Die Auswahl der geeigneten Methode hängt auch von den zur Verfügung stehenden Informationen ab. Beispielsweise hängt die im vorherigen Kapitel ermittelte Federkonstante von drei Größen ab:

1. der Masse \(m\), die mit einer Küchenwaage ermittelt wurde, deren Ablesegenauigkeit mit \(e_r(m) = 0,5 g = 0,0005 kg\) geschätzt wird.

2. dem Abstand zum Gewicht bzw. nach der Aufbereitung der Daten der Ausdehnung der Feder \(\Delta x\), die mit einem elektronischen Abstandssensor und einem Arduino ermittelt wurden (Ultrasonic Ranging Module HC - SR04).

   • Die Ablesegenauigkeit des Messsystems beträgt eine Einheit der Messauflösung, also \(e_{r} = 0,01 cm = 0,0001 m\).
   • Die Messabweichung des Messsystems beträgt laut Datenblatt bis zu 3 mm, die symmetrisch zu verstehen ist, also \(e_{r} = 3 mm = 0,003 m\).
   • Die zufällige Komponente der Messabweichung beträgt also \(e_r(x) = 0,0001 m + 0,003 m = 0,0031m\)

3. der statistischen Schätzung der Federkonstante \(k = \frac{m \cdot g}{\Delta x} = 33,019 \pm 0,378\) bzw. im festgelegten Vertrauensintervall \(k_{95\%} = 32,269 ≤ 33,019 ≤ 33,769\).

Hinweis 4.4: Formelzeichen und Einheiten

Im Folgenden werden identische Zeichen für Sekunde und Strecke \(s\), Masse und Meter \(m\), Gramm und die Konstante \(g\) sowie \(\Delta\) für die Veränderung einer Größe und den Größtfehler verwendet. Die Formeln sollten also mit großer Aufmerksamkeit gelesen werden.

1. Fehlerabschätzung

Die Fehlerabschätzung wird verwendet, wenn

• eine Größe
• nur einmal

gemessen wird.

Da der wahre Wert einer Messgröße unbekannt ist, bezweckt die Fehlerabschätzung, die maximal mögliche Abweichung des Messwerts vom tatsächlichen Wert, also den Größtfehler, zu bestimmen. Bei einer einmaligen Messung gibt es keine statistische Komponente. In die Fehlerabschätzung eines einzelnen Messwerts gehen deshalb ein:

• die Garantiefehlergrenze des Messgerätes, die vom Hersteller auf dem Gerät oder in der Bedienungsanleitung angegeben ist (siehe Beispiel), also die bekannte systematische Messabweichung \(e_{s,b}\), und
• ein abgeschätzter Anteil, der sich nach den konkreten Bedingungen des Experiments, etwa der Skalenteilung des Messgerätes oder den Ablesebedingungen richtet. Dieser Anteil kann also aus einem systematischen Anteil (bspw. eine analoge Skala konnte nur aus einem Winkel abgelesen werden) und einem zufälligen Anteil (bspw. Ablesegenauigkeit des Messgeräts) bestehen.

Der Größtfehler \(\Delta x\) ergibt sich aus der Addition der Beträge der bekannten systematischen Messabweichung und der geschätzten zufälligen Messabweichung: \(\Delta x = |e(x)_{s,b}| + |e(x)_{r}|\).

(Hempel (2016), S. 3)

Aufgabe Temperaturmessung

Mit einem digitalen Thermometer und einem thermoelektrischen Element vom Typ K wurde die Temperatur \(T = 112,1 ~ °C\) gemessen. Welche systematischen und zufälligen Messabweichungen sind bekannt und können angegeben werden (siehe Beispiel)?

Beispiel 4.2: Garantiefehlergrenze Thermometer

Thermometer

Spezifikationen

Tipp 4.3: Halber oder ganzer Skalenstrich?

Messgeräte mit digitaler Anzeige machen es leicht: Die Ablesegenauigkeit beträgt eine Skaleneinheit. Bei Messgeräten mit analoger Anzeige ist es Ermessenssache, welche Messgenauigkeit Sie angeben können bzw. möchten.

Sind Sie sich absolut sicher, dass Sie zwischen “genau auf dem Strich” und “zwischen zwei Strichen” unterscheiden können, beträgt Ihr Ablesefehler einen halben Skalenstrich. Sind Sie sich nicht sicher, beträgt Ihr Ablesefehler einen ganzen Skalenstrich.

(Fehlerrechnung leicht gemacht, FSU Jena)

Tipp 4.4: Musterlösung Temperaturmessung

systematische Messabweichung

Die absolute Messabweichung beträgt \(u(T) = 0,3 ~ °C\). Die relative Messabweichung beträgt \(0,05 ~ \%\). Das bedeutet:

\(\frac{u(T)}{112,1 °C} \cdot 100 ~ \% = 0,05 ~ \%\)

\(\frac{u(T)}{112,1 °C} \cdot 100 = 0,05\)

\(u(T) = 0,05 \cdot \frac{112,1 °C}{100}\)

\(u(T) = 0,05605 °C\)

Die bekannte systematische Messabweichung beträgt also:

\(e(T)_{s,b} = 0,3 ~ °C+ 0,05605 ~ °C = 0,35605 ~ °C\)

zufällige Messabweichung

Die zufällige Messabweichung beträgt eine Skaleneinheit, also:

\(e(T)_{r} = 0,1 ~ °C\)

Größtfehler

Der Größtfehler beträgt:

\(\Delta T = |e(T)_{s,b}| + |e(T)_{r}|\)

Die Messunsicherheit ist auf zwei Stellen aufzurunden:

\(\Delta T = |0,35605 °C| + |0,1 ~ °C| = 0,45605 ~ °C \approx 0,46 °C\)

Das vollständige Messergebnis lautet also \(T = 112,1 \pm 0,46 ~ °C\).

Beispiel Messbedingungen

Was ist mit den konkreten Bedingungen eines Messvorgangs gemeint? Das soll mit zwei einfachen Messvorgängen demonstriert werden.

Hier können Sie mitmachen!

Sie benötigen:

• ein geeignetes Messinstrument, z. B. ein Lineal, und
• eine Münze (idealerweise 1-Euro-Münze).

Im ersten Messvorgang soll der Durchmesser der 1-Euro-Münze bestimmt werden.

Beispiel 4.3: Erster Messvorgang Münze

Die Messung wird mit einem Messschieber mit Nonius 0,05 mm nach DIN 862 durchgeführt. Die DIN 862 normiert symmetrische Fehlergrenzen von Messschiebern. Die Fehlergrenze ist abhängig von der Skalengenauigkeit des Messschiebers sowie von der gemessenen Länge und ist aus einer Tabelle abzulesen. (DIN 862 wurde 2011 durch DIN EN ISO 13385-1 ersetzt, in der der Begriff der Abweichung verwendet wird. Die DIN 862 ist aber auf dem Messschieber aufgedruckt.)

Messwert: \(x = 23,25 mm\)

• Die Skaleneinteilung ist 0,05 mm, die zufällige Ableseabweichung \(e_r\) beträgt also \(\pm 0,025 mm\).
• Die DIN 862 normiert Fehlergrenzen, die abhängig von der gemessenen Länge zunehmen, mindestens aber 50 \(\mu m\) oder 0,05 mm betragen. Für den Messwert 23,25 mm gilt somit als bekannte systematische Messabweichung \(e_{s,b} = \pm 0,05 mm\).

Aus der Summe der Beträge ergibt sich der Größtfehler: \(\Delta x = |0,05| mm + |0,025| mm = 0,075 mm\).

Das vollständige Messergebnis, bestehend aus dem Messwert und der Messunsicherheit lautet also: \(23,25 ± 0,075 mm\). Der relative Größtfehler beträgt: \(23,25 mm ± 0,32\%\).

Im zweiten Messvorgang soll die Länge des Daumens bestimmt werden. (Der Daumen besteht anatomisch aus nur 2 Fingergliedknochen)

Beispiel 4.4: Zweiter Messvorgang Daumen

Die Messung wird erneut mit dem Messschieber durchgeführt.

Messwert: \(x = 64,70 mm\)

• Die Skaleneinteilung ist 0,05 mm, die zufällige Ableseabweichung beträgt also \(\pm 0,025 mm\).
• Die von der DIN 862 für gemessene Längen zwischen 50 und 300 mm normierte Fehlergrenze beträgt 50 \(\mu m\) oder 0,05 mm. Für den Messwert 64,7 mm gilt somit die Fehlergrenze \(\pm 0,05 mm\).
• zusätzlich wird eine symmetrische Messabweichung von 3 mm veranschlagt, da
  • das Messgerät nicht gerade angesetzt,
  • die Daumenwurzel nicht exakt lokalisiert und
  • die elastische Fingerkuppe nicht fixiert werden konnte.

Aus der Summe der Beträge ergibt sich der Größtfehler \(\Delta x = |0,025| mm + |0,05| mm + |3| mm = 3,075 mm \approx 3,08 mm\).

Das Messergebnis, bestehend aus dem Messwert und dem Fehlerintervall lautet also: \(64,70 ± 3,08 mm\). Der relative Größtfehler beträgt: \(64,70 mm ± 4,76 \%\).

2. Fehlerstatistik

Die Fehlerstatistik wird verwendet, wenn

• eine Größe
• mehrfach

gemessen wird.

Die Fehlerstatistik ist nur dann als zuverlässig anzusehen, wenn die Messabweichung zufällig ist, die Messwerte also betragsmäßig und mit wechselndem Vorzeichen streuen. Dann ist die Messabweichung in der ermittelten Standardabweichung enthalten. Liegt jedoch eine bekannte, systematische Messabweichung vor, muss das Messergebnis entsprechend korrigiert werden \(\bar x_E = \bar x - e_{s,b}\).

Der Fehlerstatistik haben wir in vorausgehenden Kapiteln mit der statistischen Beschreibung der empirischen Streuung des Mittelwerts vorgegriffen. Zur Wiederholung:

1. Legen Sie ein Signifikanzniveau \(\alpha\) bzw. ein zweiseitiges Konfidenzniveau \(1 - \frac{\alpha}{2}\) fest.
2. Bestimmen Sie den Stichprobenmittelwert \(\bar{x}\).
3. Bestimmen Sie die Stichprobenstandardabweichung \(s\), die Stichprobengröße \(N\) und den empirischen Standardfehler \(\frac{s_{n-1}}{\sqrt{N}}\).
4. Bestimmen Sie die Werte der Normal- bzw. der t-Verteilung für das gewählte Konfidenzniveau - für einen zweiseitigen Hypothesentest \(\frac{\alpha}{2}\) und \(1 - \frac{\alpha}{2}\)
5. Berechnen Sie das Konfidenzintervall \(\bar{x} \pm t_{\alpha / 2} ~ \frac{s_{n-1}}{\sqrt{n}}\).

Dieses Konfidenzintervall sagt für eine gewählte Wahrscheinlichkeit aus, in welchem Bereich der Mittelwert einer erneut durchgeführten Messreihe oder, wenn die unbekannte systematische Messabweichung Null (oder vernachlässigbar) ist, der wahre Wert liegen wird.
Dagegen gibt die Standardabweichung \(s\) Auskunft darüber, in welchem Bereich ein einzelner Messwert liegen wird. Die Sicherheit dieser Aussage kann durch Ausweitung des Konfidenzintervalls erhöht werden (bspw. \(2 \cdot s\)).

(Hempel 2016, 3–7)

Im folgenden Beispiel wird das Vorgehen gezeigt. Dabei wird auch die Pandas-Methode .sem() zur einfachen Berechnung des Standardfehlers vorgestellt.

Beispiel 4.5: Fehlerstatistik

Aus dem im vorherigen Kapitel behandelten Experiment wird die Messreihe für das Gewicht 503g ausgewählt.

dateipfad = "01-daten/hooke_data.csv"
hooke = pd.read_csv(filepath_or_buffer = dateipfad, sep = ';')
hooke.drop(index = 113, inplace = True) # Fehlwert, siehe vorheriges Kapitel

hooke_503g = hooke.loc[hooke['mass'] == 503, :]
print(hooke_503g.head(), hooke_503g.describe(), sep = "\n\n")

    no  mass  distance
40  40   503    158.43
41  41   503    158.43
42  42   503    158.60
43  43   503    158.76
44  44   503    159.05

             no   mass    distance
count  10.00000   10.0   10.000000
mean   44.50000  503.0  159.314000
std     3.02765    0.0    0.781099
min    40.00000  503.0  158.430000
25%    42.25000  503.0  158.640000
50%    44.50000  503.0  159.220000
75%    46.75000  503.0  159.965000
max    49.00000  503.0  160.610000

Betrachten wir für diese Messreihe noch einmal das arithmetische Mittel (das unbereinigte Messergebnis) und den Standardfehler des Mittelwerts (das statistische Streuungsmaß des Mittelwerts). Die Methode .sem() berechnet den empirischen Standardfehler des Mittelwerts (standardmäßig ist der Parameter ddof = 1 gesetzt.)

Ausgabe auf 3 Dezimalstellen genau.

print(f"Gewicht in Gramm: {hooke_503g['mass'].unique()}",
      f"Mittelwert der Messwerte: {hooke_503g['distance'].mean():.3f} cm",
      f"empirischer Standardfehler: {hooke_503g['distance'].sem():.3f} cm",
      sep = "\n")

Gewicht in Gramm: [503]
Mittelwert der Messwerte: 159.314 cm
empirischer Standardfehler: 0.247 cm

Die Messunsicherheit wird auf 2 Dezimalstellen genau aufgerundet. Dafür kann die NumPy-Funktion np.ceil() verwendet werden. Diese rundet allerdings zur nächsten Ganzzahl, ein Parameter, um auf eine bestimmte Dezimalstelle zu runden, ist nicht verfügbar. Deshalb muss die Dezimalstelle um die gewünschte Anzahl Stellen durch Multiplikation mit der entsprechenden Zehnerpotenz verschoben werden. Für 2 Dezimalstellen entsprechend um \(10^2\): np.ceil(wert * 100) / 100.

wert = pd.Series([0.247])
print(np.ceil(wert * 100) / 100)

# mit Pandas-Methoden
print(wert.mul(100).apply(np.ceil).div(100))

0    0.25
dtype: float64
0    0.25
dtype: float64

Für die Verkettung mit weiteren Methoden in Pandas muss die Rückgabe der Funktion, ein NumPy-Skalar oder -Array, wieder in eine pd.Series umgewandelt werden.

print(f"Gewicht in Gramm: {hooke_503g['mass'].unique()}",
      f"Mittelwert der Messwerte: {hooke_503g['distance'].mean():.3f} cm",
      f"empirischer Standardfehler: { ( sem_hooke_503g:= pd.Series(hooke_503g['distance'].sem()).mul(100).apply(np.ceil).div(100) ).item() :.3f} cm",
      f"vollständiges Messergebnis: {hooke_503g['distance'].mean().round(2):.2f} cm ± {sem_hooke_503g.item()} cm",
      sep = "\n")

Gewicht in Gramm: [503]
Mittelwert der Messwerte: 159.314 cm
empirischer Standardfehler: 0.250 cm
vollständiges Messergebnis: 159.31 cm ± 0.25 cm

Zusätzliche Angabe des 95-%-Konfidenzintervalls.

# t-Wert bestimmen für Signifikanzniveau (alpha-Niveau) 1 - 95 % wählen
alpha = 0.05
n = hooke_503g.shape[0] # Anzahl Zeilen
t_wert = scipy.stats.t.ppf(q = 1 - alpha/2, df = n - 1)

print(f"95-%-Konfidenzintervall : {hooke_503g['distance'].mean().round(2)} cm  ± {t_wert:.4f} * {sem_hooke_503g.item()} cm",
f"95-%-Konfidenzintervall : {hooke_503g['distance'].mean().round(2)} cm  ± {( t_wert * sem_hooke_503g.item() ).round(2):.2f} cm",
f"untere 95-%-Intervallgrenze: {hooke_503g['distance'].mean().round(2) - round(t_wert * sem_hooke_503g.item(), 2):.2f} cm",
f"obere 95-%-Intervallgrenze: {hooke_503g['distance'].mean().round(2) + round(t_wert * sem_hooke_503g.item(), 2):.2f} cm",
sep = "\n")

95-%-Konfidenzintervall : 159.31 cm  ± 2.2622 * 0.25 cm
95-%-Konfidenzintervall : 159.31 cm  ± 0.57 cm
untere 95-%-Intervallgrenze: 158.74 cm
obere 95-%-Intervallgrenze: 159.88 cm

3. Fehlerfortpflanzung

Die Fehlerfortpflanzung wird verwendet, wenn

• mehrere Eingangsgrößen,
• die durch eine Funktion die Ergebnisgröße ergeben,

gemessen werden.

Um die Messunsicherheit einer Größe \(Y\), die durch eine Funktion \(y = f(x_1, x_2, ..., x_m)\) geschätzt wird, zu ermitteln, gibt es zwei Verfahren:

• die lineare Fehlerfortpflanzung wird benutzt, wenn die Unsicherheit der beteiligten Größen durch Fehlerabschätzung einer Einzelmessung ermittelt wurden.
• die Gauß’sche Fehlerfortpflanzung wird benutzt, wenn die Unsicherheit aus einer Mehrfachmessung statistisch ermittelt und mit Konfidenzintervallen angegeben werden.

(Hempel 2016, 8–9)

Lineare Fehlerfortpflanzung

Die lineare Fehlerfortpflanzung betrachtet, wie sich die Größtfehler mehrerer gemessener Größen im ungünstigsten Fall auswirken. Es wird also der Größtfehler der gesuchten Größe \(Y\) berechnet. (vgl. Deutsches Institut für Normung (1996), S. 9)

Für eine Funktion mit zwei Eingangsgrößen \(f = f(x_1, x_2)\) wird der Größtfehler \(\Delta f\) aus den Größtfehlern \(\Delta x_1\) und \(\Delta x_2\) ermittelt.

\[ f + \Delta f = f(x_1 + \Delta x_1, x_2 + \Delta x_2) \]

Unter der Voraussetzung gegenüber den Messwerten kleiner Fehler (Wann sind die Fehler klein?) kann der Fehler \(\Delta f\) durch die Beträge der partiellen Ableitung des ersten Glieds der Taylorreihe berechnet werden (siehe Beispiel).

\[ f + \Delta f = f(x_1, x_2) + | \frac{\partial f(x_1, x_2)}{\partial x_1} | \cdot \Delta x_1 + | \frac{\partial f(x_1, x_2)}{\partial x_2} | \cdot \Delta x_2 \]

Beispiel 4.6: Taylorreihe

Die Taylorreihe - einfach erklärt von Denkbar ist abrufbar auf YouTube. 2015

Beispiel 4.7: Partielle Ableitung

Die partielle Ableitung ist die Ableitung einer Funktion mit mehreren Variablen nach einer Variablen, wobei die übrigen Variablen als Konstanten behandelt werden.

Für eine Funktion \(f(x, y) = 2x + y^2\) wird die partielle Ableitung nach x so ausgedrückt:

\(\frac{\partial f(x, y)}{\partial x}\)

• Das Symbol ∂ ist die kursive Darstellung des kyrillischen Kleinbuchstaben д (d) und wird als “del” gelesen. Es zeigt an, das eine partielle Ableitung durchgeführt wird.
• Im Zähler steht die Funktion, die abgeleitet werden soll. Im Nenner steht die Variable nach der abgeleitet wird. Der Term wird gelesen als “del f von x und y nach del x”.

Die partielle Ableitung \(\frac{\partial f(x, y)}{\partial x} = 2\). \(y^2\) wird als Konstante behandelt (z. B. \(5^2\) ) und ist abgeleitet Null.

Die partielle Ableitung \(\frac{\partial f(x, y)}{\partial y} = 2y\). \(2x\) wird als Konstante behandelt (z. B. \(2 \cdot 3\) ) und ist abgeleitet Null.

Der Größtfehler ergibt sich aus: \[ \Delta f = | \frac{\partial f(x_1, x_2)}{\partial x_1} | \cdot \Delta x_1 + | \frac{\partial f(x_1, x_2)}{\partial x_2} | \cdot \Delta x_2 \]

(Hempel 2016, 9–10)

Bzw. in Kurzschreibweise für \(i = N\) Eingangsgrößen: \[ \Delta f(x_i) = \pm \sum_{i=1}^{N} | \frac{\partial f}{\partial x_i} \cdot \Delta x_i | \]

(nach Eden und Gebhard 2024, 35, Notation angepasst)

Beispiel 4.8: Beispiel Federkonstante

Beispielhaft betrachten wir die erste Messung aus der Messreihe mit dem Gewicht 503 Gramm.

hooke_503g_einzelwert = hooke_503g.iloc[0, :].copy()
print(hooke_503g_einzelwert)

no           40.00
mass        503.00
distance    158.43
Name: 40, dtype: float64

Da mehrere Größen betrachtet werden, werden die Messwerte in eine SI-Einheit umgerechnet. Als Nullpunkt wird die erste Messung der Messreihe mit dem Gewicht 0 Gramm aufgefasst.

hooke_503g_einzelwert['mass'] = hooke_503g_einzelwert['mass'] / 1000
hooke_503g_einzelwert['distance'] = hooke_503g_einzelwert['distance'] / 100

nullpunkt = hooke[hooke['mass'] == 0].loc[: , 'distance'].head(n = 1) /100
print(f"Nullpunkt in Metern: {nullpunkt.item():.3f}\n")

hooke_503g_einzelwert['ausdehnung'] = (hooke_503g_einzelwert['distance'].item() -nullpunkt.item()) * -1
print(hooke_503g_einzelwert)

Nullpunkt in Metern: 1.733

no            40.0000
mass           0.5030
distance       1.5843
ausdehnung     0.1489
Name: 40, dtype: float64

Für die Federkonstante gilt (die Abstandsänderung \(\Delta x\) wird mit \(s\) notiert):

\[ k = \frac{m \cdot g}{\Delta{x}} = \frac{m \cdot g}{s} \]

Einsetzen der Werte (\(s\) steht nun für Sekunde, \(m\) für Meter): \[ k = \frac{0,503 kg \cdot 9,81 m}{0,1489 m \cdot s^2} = \frac{0,503 \cdot 9,81}{0,1489} \frac{N}{{m}} = 33.139 \frac{N}{{m}} \]

So gilt für den Größtfehler der Funktion: \[ \Delta k(m, s) = | \frac{\partial f(m, s)}{\partial m} | \cdot \Delta m + | \frac{\partial f(m, s)}{\partial s} | \cdot \Delta s \]

Im ersten Schritt werden die partiellen Ableitungen der Funktion \(k = \frac{m \cdot g}{s}\) gebildet. Die partielle Ableitung nach \(m\) lautet mit Faktorregel: \[ \frac{\partial f(m, s)}{\partial m} = \frac{\partial}{\partial m} \frac{m \cdot g}{s} = \frac{\partial}{\partial m} m \cdot \frac{g}{s} = 1 \cdot \frac{g}{s} = \frac{g}{s} \]

Die partielle Ableitung nach s lautet: \[ \frac{\partial f(m, s)}{\partial s} = \frac{\partial}{\partial s} \frac{m \cdot g}{s} = - \frac {m \cdot g}{s^{2}} \]

Der Größtfehler ergibt sich also durch: \[ \Delta k = | \frac{g}{s} | \cdot \Delta m ~ + ~ | (-) \frac {m \cdot g}{s^{2}} | \cdot \Delta s \]

Im zweiten Schritt wird der Größtfehler der beteiligten Größen ermittelt.

• Die Masse \(m\) der verwendeten Gewichte wurde mit einer Küchenwaage ermittelt, deren Ableseabweichung auf \(e_r (m) = 0,5 g = 0,0005 kg\) geschätzt wird. Eine systematische Messabweichung ist nicht bekannt.
  Der Größtfehler der Masse beträgt also \(\Delta m = 0,0005 kg\).
• Der Größtfehler der Abstandsmessung beträgt \(e_{r}(s) = 0,01 cm + 0,3 cm = 0,0031 m\).

Die Messwerte, die Konstante \(g\) und die Größtfehler werden eingesetzt. \[ \Delta k = | \frac{9,81 m}{{s}^2 \cdot 0,1489 m} | \cdot 0,0005 kg ~ + ~ | (-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot (0,1489 m)^2} | \cdot 0,0031 m \]

Trennen von Werten und Einheiten: \[ \Delta k = | \frac{9,81 \cdot 0,0005}{ 0,1489 } \frac{m \cdot kg}{{s}^2 \cdot m} | ~ + | (-) \frac{0,503 \cdot 9,81 \cdot 0,0031}{0,02217121} \frac{kg \cdot m^2}{{s}^2 \cdot m^2} | \]

Berechnen und Newton \(\frac{kg \cdot m}{s^2}\) einsetzen: \[ \Delta k = | 0,0329 \frac{N}{{m}} | ~ + | (-) 0,6899 \frac{N \cdot m}{{m^2}} | \]

Meter im zweiten Term kürzen: \[ \Delta k = |0,0329 \frac{N}{{m}} | ~ + | (-) 0,6899 \frac{N}{{m}} | \]

Die Messunsicherheit wird auf zwei Dezimalstellen aufgerundet. \[ \Delta k = 0,7228 \frac{N}{{m}} \approx 0,73 \frac{N}{{m}} \]

Das vollständige Messergebnis lautet somit: \[ k = 33,14 \frac{N}{m}; \Delta k = 0,73 \frac{N}{{m}} \]

Gauß’sche Fehlerfortpflanzung

Bei der Gauß’schen Fehlerfortpflanzung wird unterstellt, dass sich die Messunsicherheiten der beteiligten Größen teilweise kompensieren können. Dadurch wird eine realistischere Abschätzung der Messunsicherheit erreicht.

Die Ermittlung der Messunsicherheit ist in DIN 1319-3 geregelt. Für eine Funktion \(Y = f(x_1, x_2, ..., x_m)\) ermittelt sich die Messunsicherheit aus der Messunsicherheit der beteiligten Größen. Dazu werden die Varianzen der Mittelwerte verwendet (Deutsches Institut für Normung (1996), Gleichung (29), S. 11). \[ u^2(x_i) = s^2(\bar{x_i}) = s_i^2/n_i ~ ; ~ s_i^2 = \frac{1}{n_i - 1} \sum_{j = 1}^{n_i} (x_{ij - \bar{x_i}})^2 \]

Hinweis: In der Regel wird man die empirische Standardabweichung \(s_{n-1}\) verwenden.
Hinweis: In der DIN wird der arithmetische Mittelwert einer Messreihe statt mit \(\bar{x}\) mit \(\bar{v}\) geschrieben.

Die Messunsicherheit der beteiligten Größen wird also über den Standardfehler des Mittelwerts der beteiligten Größen ermittelt: \[ u(x_i) = s_i/\sqrt{n_i} \]

Hinweis: In der Regel wird man die empirische Standardabweichung \(s_{n-1}\) verwenden.

(Deutsches Institut für Normung 1996, 11)

Die Unsicherheit der Funktion \(y = f(x_1, x_2, ..., x_m)\) berechnet sich wie folgt (DIN 1319-3, Gleichung (43)):

\[ u(y) = \sqrt{\sum_{i = 1}^{m} (\frac{\partial f}{\partial x_i})^2 \cdot u^2(x_i)} \]

Die quadrierten Terme können auch zusammengefasst werden:

\[ u(y) = \sqrt{\sum_{i = 1}^{m} \left(\frac{\partial f}{\partial x_i} \cdot u(x_i)\right)^2} \]

Für eine Funktion mit zwei Eingangsgrößen \(y = f(x_1, x_2)\) berechnet sich die Unsicherheit der Ergebnisgröße beispielsweise wie folgt:

\[ u(y) = \sqrt{ (\frac{\partial f}{\partial x_1} \cdot \sigma_{x_1})^2 + (\frac{\partial f}{\partial x_2} \cdot \sigma_{x_2})^2 } \]

Hinweis: In der Regel wird man die empirische Standardabweichung \(s_{n-1} / \sqrt{N}\) verwenden.

Beispiel 4.9: Beispiel Messreihe 503 Gramm

Betrachten wir noch einmal die Messreihe für das Gewicht 503 Gramm. Es soll das vereinbarte Konfidenzniveau \(95 ~ \%\) gelten.

# Messdaten aus dem Kapitel hooke.qmd wiederherstellen
## Datei einlesen und Fehler entfernen
dateipfad = "01-daten/hooke_data.csv"
hooke = pd.read_csv(filepath_or_buffer = dateipfad, sep = ';')
hooke.drop(index = 113, inplace = True)

## Abstandsmessung auf Nullpunkt normieren
nullpunkt = hooke[hooke['mass'] == 0].loc[: , 'distance'].mean()
hooke['ausdehnung'] = hooke['distance'].sub(nullpunkt).mul(-1)

# Messreihe 503 Gramm auswählen
hooke_503g = hooke.loc[hooke['mass'] == 503, :].copy()

## Masse in kg, Abstand und Ausdehnung in m umrechnen
hooke_503g['mass'] = hooke_503g['mass'].div(1000)
hooke_503g['distance'] = hooke_503g['distance'].div(100)
hooke_503g['ausdehnung'] = hooke_503g['ausdehnung'].div(100)

# t-Wert bestimmen für Signifikanzniveau (alpha-Niveau) 1 - 95 % wählen
alpha = 0.05
n_ausdehnung = hooke_503g.shape[0] # Anzahl Zeilen
t_wert_ausdehnung = scipy.stats.t.ppf(q = 1 - alpha/2, df = n_ausdehnung - 1)

# Ausgabe
print(f"Gewicht in Kilogramm: {hooke_503g['mass'].unique()}",
      f"Mittlere Ausdehnung: {hooke_503g['ausdehnung'].mean():.4f} m",
      f"empirischer Standardfehler: { (sem_hooke_503g:= pd.Series(hooke_503g['ausdehnung'].sem())).item() :.6f} m",
      f"t-Wert der Ausdehnung: {t_wert_ausdehnung:.4f}",
      f"95-%-Intervallgrenzen: {(hooke_503g['ausdehnung'].mean() - t_wert_ausdehnung * sem_hooke_503g).item():.4f} m ≤ {hooke_503g['ausdehnung'].mean():.4f} m ≤ {(hooke_503g['ausdehnung'].mean() + t_wert_ausdehnung * sem_hooke_503g).item():.4f} m",
      sep = "\n")

Gewicht in Kilogramm: [0.503]
Mittlere Ausdehnung: 0.1432 m
empirischer Standardfehler: 0.002470 m
t-Wert der Ausdehnung: 2.2622
95-%-Intervallgrenzen: 0.1376 m ≤ 0.1432 m ≤ 0.1488 m

Für die Federkonstante gilt (die Abstandsänderung \(\Delta x\) wird mit \(s\) notiert):
\[ k = \frac{m \cdot g}{\Delta{x}} = \frac{m \cdot g}{s} \]

\[ k = \frac{0,503 kg \cdot 9,81 m}{0,1432 m \cdot s^2} = \frac{0,503 \cdot 9,81}{0,1432} \frac{N}{{m}} = 34,458\frac{N}{{m}} \]

 

Um die Unsicherheit der Ergebnisgröße \(k\) nach der Gauß`schen Fehlerfortpflanzung zu bestimmen, müsste die Masse des verwendeten Gewichts ebenfalls durch eine Messreihe bestimmt worden sein. (Wie Messreihen und Einzelmessungen kombiniert werden können, wird im nächsten Abschnitt gezeigt.) Deshalb wird angenommen, dass mehrere Messungen zur Ermittlung des Gewichts durchgeführt wurden. Die Messreihe sowie ihr Mittelwert und Standardfehler könnten wie folgt aussehen:

messreihe_503g = pd.Series([503 , 503, 504, 502, 503, 502, 503, 504])
messreihe_503g /= 1000

# t-Wert bestimmen für Signifikanzniveau (alpha-Niveau) 1 - 95 % wählen
alpha = 0.05
n_masse = messreihe_503g.shape[0] # Anzahl Elemente
t_wert_masse = scipy.stats.t.ppf(q = 1 - alpha/2, df = n_masse - 1)

# Ausgabe
print(f"arithmetisches Mittel der Masse: {messreihe_503g.mean()} kg",
      f"empirischer Standardfehler: { (sem_messreihe_503g:= pd.Series(messreihe_503g.sem())).item() :.6f} kg",
      f"t-Wert der Masse: {t_wert_masse:.4f}",
      f"95-%-Intervallgrenzen: {(messreihe_503g.mean() - t_wert_masse * sem_messreihe_503g).item():.4f} kg - {(messreihe_503g.mean() + t_wert_masse * sem_messreihe_503g).item():.4f} kg",
      sep = "\n")

arithmetisches Mittel der Masse: 0.503 kg
empirischer Standardfehler: 0.000267 kg
t-Wert der Masse: 2.3646
95-%-Intervallgrenzen: 0.5024 kg - 0.5036 kg

Die Gauß’sche Fehlerfortpflanzung wird ähnlich zur linearen Fehlerfortpflanzung berechnet.

\[ u(k(m, s)) = \sqrt{ (\frac{\partial f(m, s)}{\partial m} \cdot \sigma_{m})^2 + (\frac{\partial f(m, s)}{\partial s} \cdot \sigma_{s})^2 } \]

Die partiellen Ableitungen werden eingesetzt. \[ u(k(m, s)) = \sqrt{ ( \frac{g}{s} \cdot \sigma_{m})^2 + (- \frac {m \cdot g}{s^{2}} \cdot \sigma_{s})^2 } \]

Vollständiges Messergebnis

Die Messwerte, die Konstante \(g\) und die Standardfehler der Mittelwerte werden eingesetzt. \[ u(k(m, s)) = \sqrt{ ( \frac{9,81 m}{{s}^2 \cdot 0,1432 m} \cdot 0,000267 kg)^2 + ((-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot ( 0,1432 m)^2} \cdot 0,00247 m)^2 } \]

Trennen von Werten und Einheiten: \[ u(k(m, s)) = \sqrt{ ( \frac{9,81 \cdot 0,000267}{ 0,1432 } \frac{m \cdot kg}{{s}^2 \cdot m})^2 + ((-) \frac{0,503 \cdot 9,81 \cdot 0,00247}{0,02051} \frac{kg \cdot m^2}{{s}^2 \cdot m^2})^2 } \]

Berechnen, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen und Meter im 2. Term kürzen: \[ u(k(m, s)) = \sqrt{ ( \frac{9,81 \cdot 0,000267}{ 0,1432 } \frac{N}{m})^2 + ((-) \frac{0,503 \cdot 9,81 \cdot 0,00247}{0,02051} \frac{N}{m})^2 } \]

Zusammenfassen: \[ u(k(m, s)) = \sqrt{ ( 0,0183 \frac{N}{m})^2 + ((-) 0,594 \frac{N}{m})^2 } \]

Ausrechnen: \[ u(k(m, s)) = 0,595 \frac{N}{m} \approx 0,60 \frac{N}{m} \]

Das vollständige Messergebnis lautet somit: \[ k = 34,46 \frac{N}{m} \pm 0,60 \frac{N}{m} \]

95-%-Vertrauensintervall

Zusätzlich zum vollständigen Messergebnis kann ein Vertrauensintervall angegeben werden. Entsprechend der vereinbarten Vertrauenswahrscheinlichkeit, sind die entsprechenden t-Werte als Korrekturfaktoren einzusetzen.

\[ u(k(m, s)) = \sqrt{ ( \frac{g}{s} \cdot t_{\alpha/2} \cdot \sigma_{m})^2 + (- \frac {m \cdot g}{s^{2}} \cdot t_{\alpha/2} \cdot \sigma_{s})^2 } \]

Dies sind für die Masse \(t = 2,3646\) und für die Ausdehnung \(t = 2,2622\).

Die Messwerte, die Konstante \(g\), der Standardfehler des Mittelwerts und der t-Wert werden in den ersten Term eingesetzt. \[ (\frac{g}{s} \cdot t_{\alpha/2} \cdot \sigma_{m})^2 = ( \frac{9,81 m}{{s}^2 \cdot 0,1432 m} \cdot 2,3646 \cdot 0,000267 kg)^2 \]

Trennen von Werten und Einheiten, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen: \[ (\frac{9,81 \cdot 2,3646 \cdot 0,000267}{ 0,1432 } \frac{m \cdot kg}{{s}^2 \cdot m})^2 = (0,0433 \frac{N}{m})^2 \]

Die Messwerte, die Konstante \(g\), der Standardfehler des Mittelwerts und der t-Wert werden in den zweiten Term eingesetzt. \[ (- \frac {m \cdot g}{s^{2}} \cdot t_{\alpha/2} \cdot \sigma_{s})^2 = ((-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot ( 0,1432 m)^2} \cdot 2,2622 \cdot 0,00247 m)^2 \]

Trennen von Werten und Einheiten, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen und \(m\) kürzen: \[ ((-) \frac{0,503 \cdot 9,81 \cdot 2,2622 \cdot 0,00247}{0,02051} \frac{kg \cdot m^2}{{s}^2 \cdot m^2})^2 = ((-) 1,344 \frac{N}{m})^2 \]

Die Formel lautet somit: \[ u(k(m, s)) = \sqrt{ ( 0,0433 \frac{N}{m})^2 + ((-) 1,344 \frac{N}{m})^2 } \]

Ausrechnen: \[ u(k(m, s)) = 1,345 \frac{N}{m} \approx 1,35 \frac{N}{m} \]

Die Intervallgrenzen lauten somit: \[ k = 34,46 \frac{N}{m} \pm 1,35 \frac{N}{m} \]

Also: \[ k_{95\%} = 33,11 \frac{N}{m} \le 34,46 \frac{N}{m} \le 35,81 \frac{N}{m} \]

Übersicht Fehlerfortpflanzung für Grundrechenarten und Potenzprodukte

Einige Funktionen sind besonders leicht zu berechnen. In der folgenden Tabelle sind Rechenwege zur Ermittlung der Messunsicherheit nach der Gauß’schen Fehlerfortpflanzung (Standardfehler) und nach der linearen Fehlerfortpflanzung (Größtfehler) aufgelistet.

Fehlerfortpflanzung für Grundrechenarten und Potenzprodukte

(Eden und Gebhard 2024, 36)

Spezialfall: Fehlerfortpflanzung mit Einzelwerten

Ein Sonderfall ist die Ermittlung der Messunsicherheit, wenn diese sich aus statistischen Vertrauensbereichen und abgeschätzten Fehleranteilen aus einer Einzelmessung zusammensetzt.

Für die Berechnung eines Gesamtfehlers muss ein Kompromiss eingegangen werden.

1. Die lineare Fehlerfortpflanzung wird mit dem abgeschätzten Fehler und dem statistischen Vertrauensbereich durchgeführt.
2. Die Gauß’sche Fehlerfortpflanzung wird mit dem statistischen Vertrauensbereich durchgeführt und ein Fehleranteil addiert, der aus der linearen Fehlerfortpflanzung der abgeschätzten Fehler ermittelt wird.

“Beide Verfahren sind wohl gleich gut (oder schlecht) als Kompromiss in der Laborpraxis geeignet.” (Hempel (2016), S. 9)

(Hempel (2016), S. 8 - 9)

Die DIN 1319 behandelt nur die Gauß’sche Fehlerfortpflanzung. Liegt für eine Eingangsgröße nur ein einzelner Wert vor, wird dieser als Schätzwert für diese Größe verwendet. Die Unsicherheit ist aus den verfügbaren Informationen oder nach der Erfahrung, zum Beispiel aus früheren Messungen, anzusetzen. (Deutsches Institut für Normung 1996, 11)

Als Beispiel verwenden wir wieder die Messreihe für das Gewicht 503 Gramm.

Beispiel 4.10: Beispiel Federkonstante

# Ausgabe
print(f"Gewicht in Kilogramm: {hooke_503g['mass'].unique()}",
      f"Mittlere Ausdehnung: {hooke_503g['ausdehnung'].mean():.4f} m",
      f"empirischer Standardfehler: { (sem_hooke_503g:= pd.Series(hooke_503g['ausdehnung'].sem())).item() :.6f} m",
      f"t-Wert der Ausdehnung: {t_wert_ausdehnung:.4f}",
      f"95-%-Intervallgrenzen: {(hooke_503g['ausdehnung'].mean() - t_wert_ausdehnung * sem_hooke_503g).item():.4f} m ≤ {hooke_503g['ausdehnung'].mean():.4f} m ≤ {(hooke_503g['ausdehnung'].mean() + t_wert_ausdehnung * sem_hooke_503g).item():.4f} m",
      sep = "\n")

Gewicht in Kilogramm: [0.503]
Mittlere Ausdehnung: 0.1432 m
empirischer Standardfehler: 0.002470 m
t-Wert der Ausdehnung: 2.2622
95-%-Intervallgrenzen: 0.1376 m ≤ 0.1432 m ≤ 0.1488 m

Lineare Fehlerfortpflanzung

Analog zur Fehlerabschätzung ergibt sich der Größtfehler der Federkonstante durch: \[ \Delta k = | \frac{g}{s} | \cdot \Delta m ~ + ~ | (-) \frac {m \cdot g}{s^{2}} | \cdot \Delta s \]

• Die Ableseabweichung der Küchenwaage wird auf \(e_r (m) = 0,5 g = 0,0005 kg\) geschätzt. Eine systematische Messabweichung ist nicht bekannt. Der Größtfehler der Masse beträgt also \(\Delta m = 0,0005 kg\)
• Der empirische Standardfehler der Ausdehnung beträgt \(\sigma_x = 0.00247 m\) bzw. zum vereinbarten Vertrauensniveau von \(\sigma_{x 95 \%} = 0.00247 m * 2.2622 = 0,00559 m\)

Die Messwerte, die Konstante \(g\) und die Größtfehler werden eingesetzt. \[ \Delta k = | \frac{9,81 m}{{s}^2 \cdot 0,1432 m} | \cdot 0,0005 kg ~ + ~ | (-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot (0,1432 m)^2} | \cdot 0,00247 m \]

Trennen von Werten und Einheiten: \[ \Delta k = | \frac{9,81 \cdot 0,0005}{ 0,1432 } \frac{m \cdot kg}{{s}^2 \cdot m} | ~ + | (-) \frac{0,503 \cdot 9,81 \cdot 0,00247}{0,020506} \frac{kg \cdot m^2}{{s}^2 \cdot m^2} | \]

Berechnen und Newton \(\frac{kg \cdot m}{s^2}\) einsetzen: \[ \Delta k = | 0,0342 \frac{N}{{m}} | ~ + | (-) 0,594 \frac{N \cdot m}{{m^2}} | \]

Meter im zweiten Term kürzen: \[ \Delta k = |0,0342 \frac{N}{{m}} | ~ + | (-) 0,594 \frac{N}{{m}} | \]

Die Messunsicherheit wird auf zwei Dezimalstellen aufgerundet. \[ \Delta k = 0,628 \frac{N}{{m}} \approx 0,63 \frac{N}{{m}} \]

Das Messergebnis und der Größtfehler lauten somit: \[ k = 34,46 \frac{N}{m}; \Delta k = 0,63 \frac{N}{{m}} \]

Gauß’sche Fehlerfortpflanzung

Die Unsicherheit der Federkonstante berechnet sich durch: \[ u(k(m, s)) = \sqrt{ ( \frac{g}{s} \cdot \Delta m)^2 + (- \frac {m \cdot g}{s^{2}} \cdot \sigma_{s})^2 } \]

Die Messwerte, die Konstante \(g\) und der abgeschätzte Fehleranteil (Größtfehler) der Masse werden in den ersten Term eingesetzt. \[ (\frac{g}{s} \cdot \Delta m)^2 = ( \frac{9,81 m}{{s}^2 \cdot 0,1432 m} \cdot 0,0005 kg)^2 \]

Trennen von Werten und Einheiten, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen: \[ (\frac{9,81 \cdot 0,0005}{ 0,1432 } \frac{m \cdot kg}{{s}^2 \cdot m})^2 = (0,0342 \frac{N}{m})^2 \]

Die Masse des Gewichts, die Konstante \(g\) und der Standardfehler des Mittelwerts der Ausdehnung werden in den zweiten Term eingesetzt. \[ (- \frac {m \cdot g}{s^{2}} \cdot \sigma_{s})^2 = ((-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot ( 0,1432 m)^2} \cdot 0,00247 m)^2 \]

Trennen von Werten und Einheiten, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen und \(m\) kürzen: \[ ((-) \frac{0,503 \cdot 9,81 \cdot 0,00247}{0,02051} \frac{kg \cdot m^2}{{s}^2 \cdot m^2})^2 = ((-) 0,594 \frac{N}{m})^2 \]

Die Formel lautet somit: \[ u(k(m, s)) = \sqrt{ ( 0,0342 \frac{N}{m})^2 + ((-) 0,594 \frac{N}{m})^2 } \]

Ausrechnen: \[ u(k(m, s)) = 0,595 \frac{N}{m} \approx 0,60 \frac{N}{m} \]

Das vollständige Messergebnis lautet somit: \[ k = 34,46 \frac{N}{m}; \Delta k = 0,60 \frac{N}{{m}} \]

Für das 95-%-Konfidenzintervall wird der t-Wert der Ausdehnung \(t = 2,2622\) eingesetzt. \[ u(k(m, s)) = \sqrt{ ( \frac{g}{s} \cdot \Delta m)^2 + (- \frac {m \cdot g}{s^{2}} \cdot t_{\alpha/2} \cdot \sigma_{s})^2 } \]

Der erste Term lautet unverändert:

\[ (\frac{g}{s} \cdot \Delta m)^2 = ( \frac{9,81 m}{{s}^2 \cdot 0,1432 m} \cdot 0,0005 kg)^2 = ( 0,0342 \frac{N}{m})^2 \]

Die Masse, die Konstante \(g\), der Standardfehler des Mittelwerts der Ausdehnung und der t-Wert der Ausdehnung \(t = 2,2622\) werden in den zweiten Term eingesetzt. \[ (- \frac {m \cdot g}{s^{2}} \cdot t_{\alpha/2} \cdot \sigma_{s})^2 = ((-) \frac{0,503 kg \cdot 9,81 m}{{s}^2 \cdot ( 0,1432 m)^2} \cdot 2,2622 \cdot 0,00247 m)^2 \]

Trennen von Werten und Einheiten, Newton \(\frac{kg \cdot m}{s^2}\) einsetzen und \(m\) kürzen: \[ ((-) \frac{0,503 \cdot 9,81 \cdot 2,2622 \cdot 0,00247}{0,02051} \frac{kg \cdot m^2}{{s}^2 \cdot m^2})^2 = ((-) 1,344 \frac{N}{m})^2 \]

Die Formel lautet somit: \[ u(k(m, s)) = \sqrt{ ( 0,0342 \frac{N}{m})^2 + ((-) 1,344 \frac{N}{m})^2 } \]

Ausrechnen: \[ u(k(m, s)) = 1,344 \frac{N}{m} \approx 1,35 \frac{N}{m} \]

Die Intervallgrenzen lauten somit: \[ k_{95\%} = 33,11 \frac{N}{m} \le 34,46 \frac{N}{m} \le 35,81 \frac{N}{m} \]

Deutsches Institut für Normung. 1995. Grundlagen der Meßtechnik - Teil 1: Grundbegriffe. DIN Media. https://doi.org/10.31030/2713411.

———. 1996. Grundlagen der Meßtechnik - Teil 3: Auswertung von Messungen einer einzelnen Meßgröße, Meßunsicherheit. DIN Media. https://doi.org/10.31030/7204542.

Dinter, Ralf. 2011. „Fehlerrechnung für Einsteiger. Eine beispielorientierte Einführung für Studierende der TUHH“. https://www2.physnet.uni-hamburg.de/TUHH/Versuchsanleitung/Fehlerrechnung.pdf.

Eden, Klaus, und Hermann Gebhard. 2024. Dokumentation in der Mess- und Prüftechnik: Messen - Auswerten - Darstellen Protokolle - Berichte - Präsentationen. 3. Auflage. https://doi.org/10.1007/978-3-658-44779-3.

Hempel, Rainer. 2016. „Script zur Einführung in die Grundlagen der Fehlerrechnung“. https://www.tu-braunschweig.de/index.php?eID=dumpFile&t=f&f=45992&token=b041478add5f7a3e136b69905b72bfa0e192d82b.

Hochschule Aalen. 2016. „Anleitung zur Fehlerrechnung im Physikpraktikum“. https://www.hs-aalen.de/uploads/mediapool/media/file/13430/F_Fehlerrechnung.pdf.

Schrüfer, Elmar, Leonhard M. Reindl, und Bernhard Zagar. 2022. Elektrische Messtechnik: Messung elektrischer und nichtelektrischer Größen. 13. Aufl. München: Carl Hanser Verlag.